調和級数と交代調和級数

調和級数

$a_n=1/n$ を順に足し加えていく級数を調和級数 (harmonic series)とよびます。
 \[H=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\:\cdots\:+\frac{1}{n}+\:\cdots\]
調和級数は発散します。以下に 2 通りの証明を載せておきます。

調和級数が発散することの証明①

級数の各項を $1$ 個、$2$ 個、$4$ 個 … というように $2^k$ 個ごとのグループに分けて不等号をつくります。
 \[\begin{align*}H&=1+\left(\frac{1}{2}+\frac{1}{3}\right) +\left(\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}\right)+\:\cdots\\[6pt]
&\gt 1+\left(\frac{1}{4}+\frac{1}{4}\right) +\left(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}\right)+\:\cdots\\[6pt]&=1+\frac{1}{2}+\frac{1}{2}+\:\cdots\end{align*}\]
$1/2$ を加えていく級数は発散するので、調和級数 $H$ は発散します。

調和級数が発散することの証明②

下図のように $y=1/x$ の積分と比較する方法もあります。
 

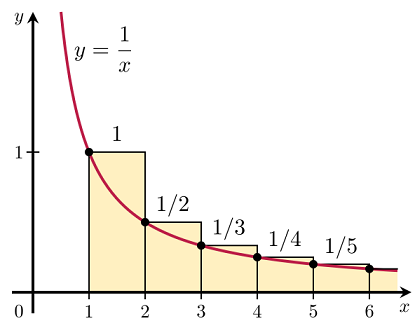
図の長方形を加えた面積が $\displaystyle \sum_{n=1}^{n}\frac{1}{n}$ に相当します。この部分が $y=1/x$ の積分より大きいのは明らかです。$y=1/x$ を 1 から ∞ まで積分すると
 \[\int_{1}^{\infty}\frac{dx}{x}=\left[\log x\right]_{1}^{\infty}=\infty\]
なので調和級数 $H$ は発散します。また有限区間において
 \[H_n=\sum_{n=1}^{n}\frac{1}{n}\gt \int_{1}^{n+1}\frac{dx}{x}=\log (n+1)\]
という関係が成り立っています。

交代調和級数

調和級数において各項の符号を交互に変えた交代級数
 \[S=1-\frac{1}{2}-\frac{1}{3}+\frac{1}{4}-\frac{1}{5}+\:\cdots\]
のことを交代調和級数（alternating harmonic series）とよびます。実はこの級数は対数関数と結びついています。$\log (1+x)$ の級数展開式
 \[\log (1+x)=\sum_{n=1}^{\infty}\frac{(-1)^{n-1}x^n}{n}\quad (-1\lt x\leq 1)\]
において $x=1$ とおくと
 \[\log 2=\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}\]
となって、これは交代調和級数そのものです。よって交代調和級数は $\log 2$ に収束します。調和級数は発散し、交代調和級数は収束するので、交代調和級数は 条件収束級数 ということになります。

【Excel】交代調和級数を調べます

Excel で描いた交代調和級数の収束の様子を載せておきます。
 

 
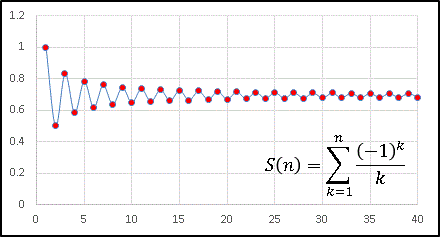
足されたり引かれたりで小刻みに変動しながらも $\log 2=0.693$ に向けて収束していく様子が見えます。

【VBA】交代調和級数を計算するプロシージャ

交代調和級数を計算する Function マクロも載せておきます。

'[VBA] 交代調和級数

Function HA(k As Integer) As Double

    Dim i As Integer, j As Integer

    If k Mod 2 = 0 Then
        i = k / 2
        j = k / 2
    Else
        i = Int(k / 2 + 1)
        j = Int(k / 2)
    End If

    For m = 1 To i
        s = s + 1 / (2 * m - 1)
    Next m

    For m = 1 To j
        s = s - 1 / (2 * m)
    Next m

    HA = s

End Function

この関数を使うときは項数 n を引数として「=HA(n)」と入力してください。