方陣算（中実方陣と中空方陣）の解き方

中実方陣と中空方陣

正方形に並べた碁石を数えるような問題を方陣算といいます。方陣という名称は戦場で兵士を四角形に並べた陣立てに由来します。方陣は大まかに分けると２種類あって、中までぎっしり詰まった並び方を中実方陣 、中を取り除いた並び方を中空方陣とよびます。まず最初に簡単な数列を使って方陣算の一般法則を確認しておきます。
 
中実方陣と中空方陣は簡単な法則で結びついています。下の図を見てください。
 

 
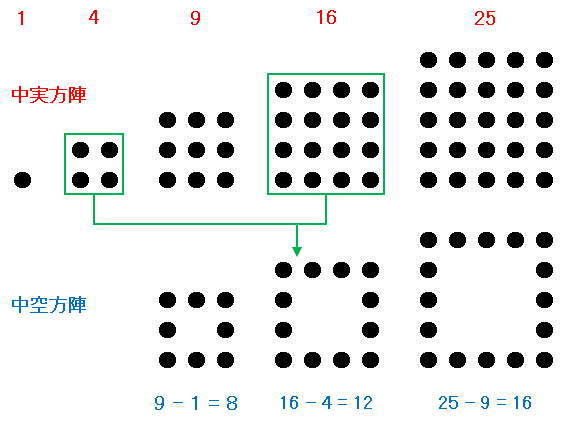
中実方陣に並んだ碁石の数は $1,\ 4,\ 9,\ 16,\ 25,\ \cdots$ というように平方数そのものです。そして一辺 $n$ 個の中空方陣の石の数は、一辺 $n$ 個の中実方陣から、一辺 $n-2$ 個の中実方陣を差し引いたものとなっています。

たとえば、上の図にあるように、一辺 $4$ 個の中実方陣の石は $16$ 個、そこから一辺 $2$ 個の中実方陣の石 $4$ 個を差し引いて、
 \[一辺\;4\;個の中空方陣の石の数\;=16-4=12\]
となっています。これを一般的な数式で書くと、一辺 $n$ 個の中空方陣の石の数 $f(n)$ は、
 \[f(n)=n^2-(n-2)^2=4(n-1)\quad(n\geq3)\]
という簡単な形で表せます。$n=5$ で確認してみると、
 \[f(5)=4\cdot(5-1)=16\]
となって、確かに上の図とぴったり合っていますね。

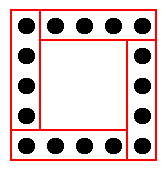これを「一辺の個数が１つ増えると、全体で４つ増える」と覚えておいてもよいかもしれません。また、中空方陣の石は次のような枠でくくって数えても同じ式が現れます。
この例では $4\times(4-1)=12$ となっていますね。
算数では基本的にこのような数え方をします。

【例題01】中空方陣

$40$ 個の碁石を中空方陣の形に並べると、一辺には何個の石が並びますか？
 
【解答1】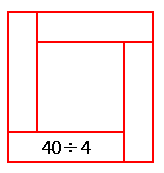図のような仕切りを作ります。１つの仕切りに $40\div 4=10$ 個の石が並ぶので、一辺の石の数は $10+1=11$ となります。
 
 
 
 
【解答2】一辺 $n$ 個の中空方陣の石の数は $4(n-1)$ なので、
 \[4(n-1)=40\]
を解いて $n=11$ となります。

【例題02】中実方陣

ある数の碁石を正方形（中実方陣）の形に並べようとしたところ、 $9$ 個も余ってしまいました。そこで $1$ 列増やした正方形に並べようとすると、今度は $4$ 個足りませんでした。碁石の数はいくつですか？
 
【解答】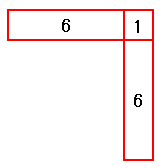余った $9$ 個と足りない $4$ 個を合わせた $13$ 個を図のように外側のＬ字に並べると、一辺が $6+1=7$ 個の中実方陣となります。石の総数は $7\times 7=49$ なのですが、ここから足りない $4$ 個を差し引くのを忘れずに。答えは $49-4=45$ 個となります。
 
 

変則方陣

ここまでは基本的な方陣を見てきましたが、変則的なバージョンもいくつかあります。たとえば周囲を二列で囲んだ中実方陣です。
 

上図のように数え方は $2$ 通りあります。$2\times 4=8$ 個に括った仕切りが $4$ つで $8\times 4=32$ 個としてもよいし、$n=4,\;6$ の中空方陣を足し加えて
 \[f(4)+f(6)=12+20=32\]
と求めることもできます。「周囲 $m$ 個で $n$ 列で囲う」ような一般的な法則を問われる問題であれば、後者の考え方のほうが解きやすいと思います。

【例題03】俵算

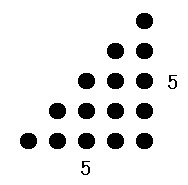右図では二辺に等しく $5$ 個ずつの直角三角形に碁石を並べています（その数は全部で $15$ 個です）。それでは二辺に等しく $n$ 個ずつの直角三角形に碁石を並べたとき、石の数は全部でいくつになりますか？　また $n=100$ の場合で計算してください。
 
 
【解答】　まず一辺が $5$ 個の場合の簡単な計算法を確認しておきます。それは右図のように全く同じ形に並んだ碁石を斜辺で組合わせてしまうというものです。つまりこの長方形に並んだ碁石の数を $2$ で割って
 \[5\times 6\div 2=15\;個\]
で計算できるということです。すると $n$ 個の場合は
 \[n(n+1)/2\;個\]
と表せます。$n=100$ のときは
 \[100(100+1)/2=5050\;個\]
となります。このような数え方を「俵算」とよびます。