旅人算（追いかけ算と出会い算）

旅人算（追いかけ算と出会い算）

複数の歩行者や車、列車などが同時に動く設定で、速度や追いつくまでの時間を求めるのが旅人算（追いかけ算と出会い算）です。中学入試や公務員試験でお馴染みのタイプの問題ですね。中にはかなり複雑な状況を設定している場合もありますが、いずれにしても基本となるのは「相対速度」という考え方です。とにかく「片方には止まっていてもらう」ことにすると、状況がずっとシンプルになります。

追いかけ算

速度の異なる物体が同じ方向に進むような問題設定を 追いかけ算 とよびます。簡単な例として下の図のように、$A$ と $B$ が互いに $30\;\mathrm{km}$ 離れた地点から同じ方向に、それぞれ
\[a=10\;\mathrm{km/h},\quad b=5\;\mathrm{km/h}\]
で同時にスタートする場合を考えてみます。図中で $A,\;B$ の速度はそれぞれ $a,\;b$ としています。



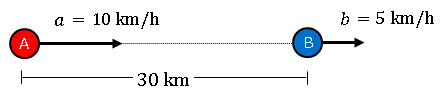
$A$ が $B$ に追いつくまでの時間を計算してみましょう。このとき「速度の遅い $B$ には止まっていてもらう」と考えて、次のような状況に置き換えます。



立ち止まっている人から見れば、この２つはどちらも動いているのですが、$A$ から見ると、止まっている $B$ に対して自分が時速 $10-5=5\;\mathrm{km}$ で移動していることになります。互いの距離は $30\;\mathrm{km}$ なので、距離を相対速度で割って
\[\frac{30\;\mathrm{km}}{5\;\mathrm{km/h}}=6\;h\]
すなわち $A$ は $6$ 時間で $B$ に追いつくことができます。

出会い算

物体同士が互いに逆向きに移動して出会う地点などを問うのが 出会い算 です。$A$ と $B$ が互いに $30\;\mathrm{km}$ 離れた地点から逆方向に（お互いに向き合う形で）それぞれ
\[a=10\;\mathrm{km/h}\quad b=5\;\mathrm{km/h}\]
で同時にスタートし、お互いが出会うまでの時間を計算してみます。



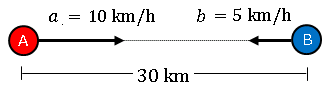
この場合は $B$ が止まっていて、$A$ が時速 $10+5=15\;\mathrm{km}$ で $B$ に向かって行くと考えます。



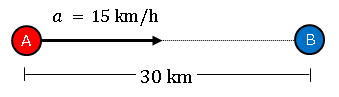
$A$ が $B$ に到達するまでにかかる時間は
\[\frac{30\;\mathrm{km}}{15\;\mathrm{km/h}}=2\;h\]
すなわち 2 時間ということになります。

円周を巡る旅人算

人や車が円周に沿って回るという状況設定の問題も定番です。たとえば次のような問題を考えてみます。

最初に $A,\;B$ が反対方向に移動する状況を考えます。
$A,\;B$ の速度をそれぞれ $a,\;b$ とします。



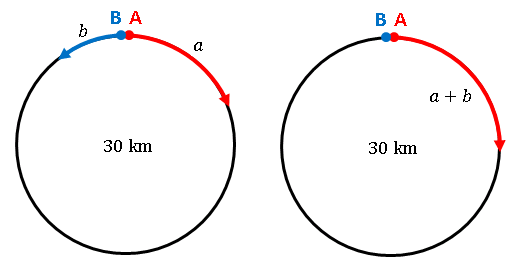
上の左図は問題の設定をそのまま書き表したもので、これを相対速度で置き換えると、右図のように $B$ は止まったままで、 $A$ が分速 $a+b\;\mathrm{km}$ で走って $18$ 分で湖を１周すると考えることができます。方程式を立てると
\[18(a+b)=30\]
両辺を $6$ で割って
\[3(a+b)=5\tag{1}\]
となります。次は $A,\;B$ が同じ方向に移動する状況です。



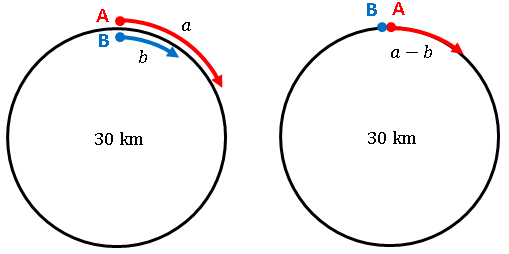
この場合も $B$ は止まっていて、$A$ が分速 $a-b\;\mathrm{km}$ で湖を１周すると考えることができるので、
\[90(a-b)=30\]
両辺を $30$ で割って
\[3(a-b)=1\tag{2}\]
(1) と (2) を解いて
\[a=1\;\mathrm{km/min},\quad b=\frac{2}{3}\;\mathrm{km/min}\]
それぞれ $60$ をかけて時速に直すと
\[a=60\;\mathrm{km/h},\quad b=40\;\mathrm{km/h}\]
となります。