【VBA】超幾何関数と楕円積分

超幾何関数

次のように定義される級数のことを超幾何級数とよびます。
\[1+\frac{ab}{c}\frac{x}{1!}+\frac{a(a+1)b(b+1)}{c(c+1)}\frac{x^2}{2!}+\cdots\:=\sum_{k=0}^{\infty}\frac{(a)_k(b)_k}{(c)_k}\frac{x^k}{k!}\]
ここで $(a)_k$ は
\[(a)_k=a(a+1)(a+2)\cdots\]
を意味する記号で、$k=0$ に対しては $(a)_0=1$ と決めておきます。この級数によって定義される関数
\[F(a,b,c\:;x)=\sum_{k=0}^{\infty}\frac{(a)_k(b)_k}{(c)_k}\frac{x^k}{k!}\]
のことを超幾何関数といいます。超幾何関数はとても広いクラスの関数であり、その中に様々な関数を内包しています。たとえば対数関数は
\[\log(1+x)=xF(1,1,2\:;-x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\cdots\quad (-1\lt x\leq 1)\]
のように表され、右辺はよく知られたマクローリン級数展開となっています。また逆三角関数も超幾何関数の１種であることが知られています。たとえば逆正弦関数は
\[\mathrm{Arcsin}x=F(1/2\:,1/2\:,3/2\:;x^2)\]
で表されます。超幾何関数は簡単な形の級数で表されているので、数値計算においてもシンプルで汎用性の高い強力なツールとなります。特に後述する完全楕円積分の計算に威力を発揮します。

超幾何関数を VBA で実装してみましょう。階乗の除算を含む級数の計算においては「巨大な数（階乗）で割るエラー」を防ぐために少し工夫する必要があります。超幾何級数
\[1+\frac{ab}{c}\frac{x}{1!}+\frac{a(a+1)b(b+1)}{c(c+1)}\frac{x^2}{2!}+\cdots\]
においては、第 2 項の係数を
\[d_2=\frac{ab}{c}\]
とおくと、第 3 項は
\[d_3=d_2\:\frac{(a+1)(b+1)}{2(c+1)}\]
となり、第 4 項は
\[d_4=d_3\:\frac{(a+2)(b+2)}{3(c+2)}\]
となります。このように１つ１つ計算させていくと、大きな数の割り算は現れにくくなり、より多くの項を計算することができます。以下に超幾何関数を計算する Function Macro（ユーザー定義関数）を載せておきます。なお、当サイトの関数を最大限に活用するため、VBA数値計算用最新コード のページに掲載されたマクロをモジュールに貼りつけることをおすすめします（以下のマクロも含んでいます）。

'[VBA]超幾何関数
Function GHGEO(a As Double, b As Double, c As Double, x As Double) As Double
　　Dim k As Integer
　　Dim fact As Long
　　Dim s As Double
　　d = a * b / c
　　s = 1 + d * x
　　For k = 2 To 100
　　　　d = d * (a + k - 1) * (b + k - 1) / (c + k - 1) / k
　　　　s = s + d * x ^ k
　　Next k
　　GHGEO = s
End Function

ちなみに、GHGEO は Gaussian Hyper Geometric Function の略です。GHGEO() を使う時は a, b, c, x の 4 つの引数を指定します。

=GHGEO(a,b,c,x)

たとえばワークシートに

=GHGEO(1,1,2,5)

と入力すると $F(1,1,2;5)$ の値が計算されます。c に 0 あるいは負整数を指定した場合にはエラーを返します。

完全楕円積分

次のような積分の形で定義される関数
\[\begin{align*}K(k)&=\int_{0}^{\pi/2}\frac{d\theta}{\sqrt{1-k^2\sin\theta}}\quad (0\leq k\leq 1)\\[6pt]E(k)&=\int_{0}^{\pi/2}\sqrt{1-k^2\sin\theta}\quad (0\leq k\leq 1)\end{align*}\]
のことを、それぞれ第１種完全楕円積分、第２種完全楕円積分とよびます。この関数は物理学で応用される関数で、$K(k)$ は振り子の周期、$E(k)$ は楕円の周長を計算するときなどに用いられます。完全楕円積分もまた超幾何関数に含まれる関数であり、それぞれ
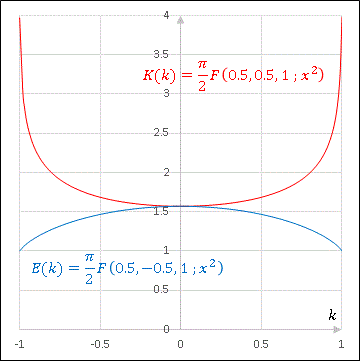
\[\begin{align*}K(k)&=\frac{\pi}{2}F\left(\frac{1}{2},\frac{1}{2},1\:;x^2\right)\\[6pt]
E(k)&=\frac{\pi}{2}F\left(\frac{1}{2},-\frac{1}{2},1\:;x^2\right)\end{align*}\]
と表されます。GHGEO関数を使って完全楕円積分のグラフを描いてみると次のようになります。