【Excel】最小二乗法と回帰直線

ある統計資料から 10 人の男性のデータを無作為抽出したら身長と体重の関係は次のようであったとします。

身長が大きければ体重も大きくなるであろうと予測できますが、太っている人も痩せている人もいますから、身長と体重はきれいな比例関係にあるわけではなく、グラフにプロットしても直線になるわけではありません。
 

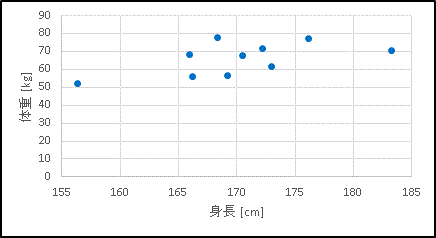
それでも、この２つのデータは近似的に直線に乗るだろうと考えて、各個のデータとの間になるべく誤差が少ないような直線を当てはめてみようというのが最小二乗法（method of least squares）の考え方です。

最小二乗法

２つの変量 $x,y$ について、大きさ $n$ の標本の組
 $$(x_1,y_1),(x_2,y_2),\cdots (x_n,y_n)$$
があり、$x$ と $y$ の間に近似的に
 $$\begin{array}{}\text{(1)}& y=ax+b\end{array}$$
という比例関係があると仮定します。$(x_i,y_i)$ と直線 (1) との誤差を
 $$\begin{array}{}\text{(2)}& e_i=y_i-(a+b{x}_i)(i=1,2,\cdots ,n)\end{array}$$
で表します。この式を線型回帰モデル（liner regression model）とよびます。(2) の i についての総和
 $$\begin{array}{}\text{(3)}& Q(a,b)=\sum _{i=1}^n{e}_i=\sum _{i=1}^n[y_i-(a+b{x}_i){]}^2\end{array}$$
が最小となるような係数 $a,b$ を決定します。すなわち
 $$\frac{\partial Q}{\partial a}=0,\frac{\partial Q}{\partial b}=0$$
となるような $a,b$ を求めます。この式に (3) を代入すると
 $$\begin{array}{}\text{(4)}& \sum _{i=1}^n{y}_i-na-b\sum _{i=1}^n{x}_i=0\end{array}$$$$\begin{array}{}\text{(5)}& \sum _{i=1}^n{x}_i{y}_i-a\sum _{i=1}^n{x}_i-b\sum _{i=1}^n{x}_i^2=0\end{array}$$
という方程式が得られます。ここで $x$ の標本平均と標本分散を $\overline{x},s_x^2$ とし、$y$ の標本平均と標本分散を $\overline{y},s_y^2$ とします。また $x$ と $y$ の標本共分散を $s_{xy}$ とします：
 $$\begin{array}{}\text{(6)}& \overline{x}& =\frac{1}{n}\sum _{i=1}^n{x}_i\text{(7)}& \overline{y}& =\frac{1}{n}\sum _{i=1}^n{y}_i\text{(8)}& s_x^2& =\frac{1}{n}\sum _{i=1}^n{x}_i^2-{\overline{x}}^2\text{(9)}& s_y^2& =\frac{1}{n}\sum _{i=1}^n{y}_i^2-{\overline{y}}^2\text{(10)}& s_{xy}& =\frac{1}{n}\sum _{i=1}^n{x}_i{y}_i-\overline{x}\overline{y}\end{array}$$
これらを全て式 (4) と (5) に入れると
$$\begin{array}{}\text{(11)}& & \overline{y}-a-b\overline{x}\text{(12)}& & s_{xy}+\overline{x}\overline{y}-\overline{x}a-(s_x^2+s_y^2)b=0\end{array}$$
となります。この式を $a,b$ について解いて、標本相関係数
 $$\begin{array}{}\text{(13)}& C_{xy}=\frac{s_{xy}}{s_x{s}_y}\end{array}$$
を定義すると
 $$\begin{array}{}\text{(14)}& a=\overline{y}-C_{xy}\overline{x}\frac{s_y}{s_x},b=C_{xy}\frac{s_y}{s_x}\end{array}$$
となります。この係数を標本回帰係数 (sample regression coefficient) とよびます。すなわち回帰直線は
 $$\begin{array}{}\text{(15)}& y-\overline{y}=C_{xy}\frac{s_y}{s_x}(x-\overline{x})\end{array}$$
で与えられます。

誤差分散と相関係数の意味

残差平方和 $Q$ を $n$ で割った
 $$s_e^2=\frac{Q}{n}=\frac{1}{n}\sum _{i=1}^n{e}_i^2$$
は誤差の分散を表しています。すなわち
 $$s_e^2=\frac{1}{n}\sum _{i=1}^n[y_i-(a+b{x}_i){]}^2$$
であり、
 $$\overline{y}-a-b\overline{x}$$
を用いて $a$ を消去すると
 $$s_e^2=\frac{1}{n}[\sum _{i=1}^n(y_i-\overline{y}{)}^2-2b\sum _{i=1}^n(x_i-\overline{x})(y_i-\overline{y})+b^2\sum _{i=1}^n(x_i-\overline{x}{)}^2]$$
という式が得られます。ここで
 $$\begin{array}{rl}& s_x^2=\frac{1}{n}\sum _{i=1}^n{x}_i^2-{\overline{x}}^2,s_y^2=\frac{1}{n}\sum _{i=1}^n{y}_i^2-{\overline{y}}^2\\ & s_{xy}=\frac{1}{n}\sum _{i=1}^n{x}_i{y}_i-\overline{x}\overline{y},b=\frac{s_{xy}}{s_x^2}\end{array}$$
を全て入れると
 $$s_e^2=s_y^2-\frac{s_{xy}^2}{s_x^2}$$
となります。$C_{xy}=s_{xy}/(s_x{s}_y)$ を用いると
 $$\begin{array}{}\text{(16)}& s_e^2=s_y^2(1-C_{xy}^2)\end{array}$$
という誤差の分散と相関係数の関係式が得られます。相関係数 $C_{xy}$ は 0 から 1 の値をとるので、その絶対値が大きいほど誤差の分散が小さくなり、２つの変量（データ）同士の関連性が強いという可能性を示しています。0 であればほぼ無関係です。ただし、相関係数はあくまで目安なので、標本の取り方によって偶然 “直線的になった” というケースもあるので注意が必要です。

また $C_{xy}$ は直線の傾きも表しています。$C_{xy}$ が正のときには「正の相関がある」、負のときには「負の相関がある」といいます。たとえば気温を $x$, ヒーターの売れ行きを $y$ とするなら、（暑い時にヒーターなんてほとんど売れないでしょうから）、そのデータには負の相関があるはずです。ちなみに記事の冒頭にある身長と体重のデータを用いて相関係数を計算すると約 0.58 となります。

【Excel】回帰直線のプロット

Excel は上で述べたような計算を全て自動で行なってくれます。記事の最初に載せてある身長と体重の表をコピーしてセル B2 に貼りつけてください。そのあとセル C3:D12 を選択した状態で [挿入] タブから [散布図] ⇒ [散布図] を選択するとグラフが表示されます。
 

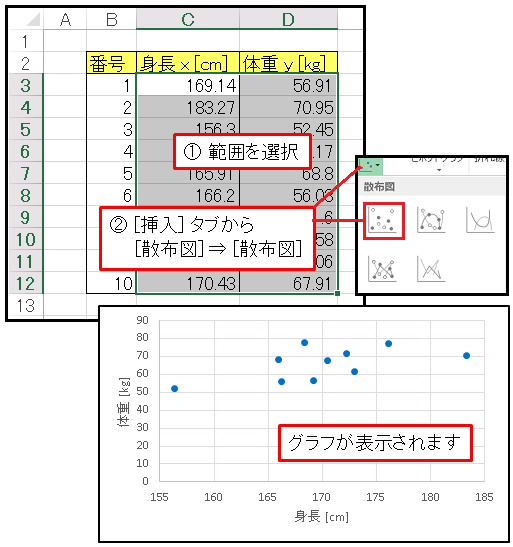
次は回帰直線を表示させてみます。散布図を右クリックして現れたメニューから [近似曲線の追加] を選択します。[近似曲線のオプション] で [線形近似] を選択してください。
 

 
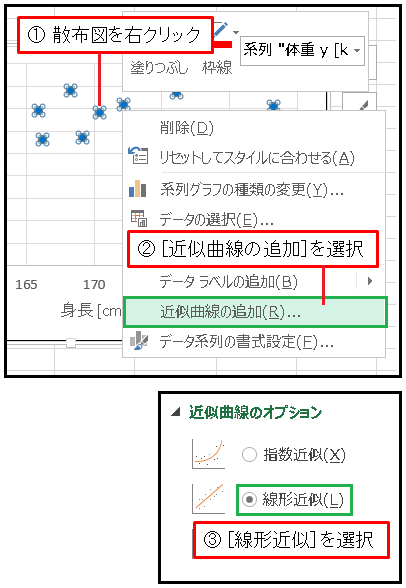
すると次のような回帰直線が表示されます。
 

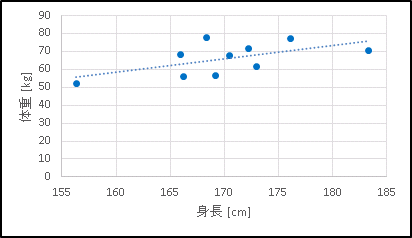
これだけでは係数の値がわからないので、数式も表示させてみましょう。近似曲線を右クリックして [近似曲線の書式設定] を選択します。[グラフに数式を表示する] にチェックを入れてください。
 

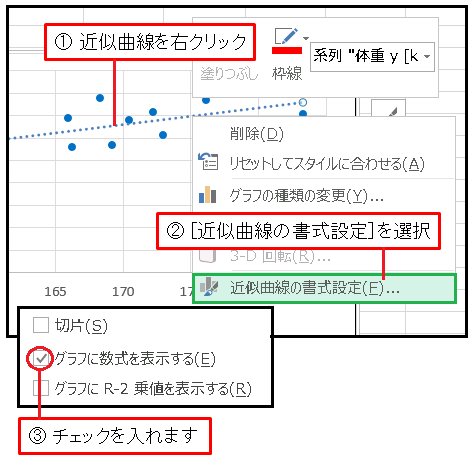
小さな文字で数式が表示されます。
 

 
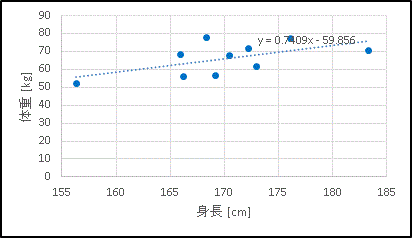
あとは回帰直線の線の色や数式の文字の大きさなどを好みに応じて適当に調整します。
 

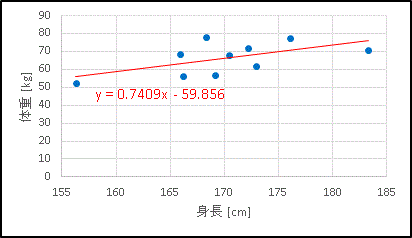
これでグラフの完成です。