整正数Nのk進展開（位取り記数法）

初等整数論講座の第 2 回目です。私たちは普段あまり意識はせずに 10 進数というものを使って数学を学んでいます。10 進数とは 10 を一束（ひとたば）と考えて数字をまとめていく方法です。1 を 10 個まとめて一束 (10) とし、その 10 を 10 個まとめて一束 (100) にし、さらに 100 を 10 個まとめて一束 (1000) とする … このようなことを繰り返して、取り得る限り最も大きな束から順に取って数字を表します。たとえば 925 という数字から取れる束の大きさは 100 ですから、それを 9 個取ります。次に残った 25 から 10 の束を 2 個取ります。最後に残った 5 は束に入らない数字ですからそのままにします。これを式で表すと

\[925=10^2\times 9+10^1\times 2+10^0\times 5\]
となります。コンピューターでは内部で数字を 0 と 1 の 2 進数で処理していますが、これは 2 を一束と考えて数字を表現しています。アナログ時計は「60 秒で繰り上がって 1 分、60 分で繰り上がって 1 時間、12 時間で繰り上がって半日」というように「 60 進数と 12 進数を組み合わせた複雑な進数システムを用いています。

高校・大学生のための整数の理論と演習 中古価格 ￥2,580から (2020/8/3 15:56時点)

整正数Nのk進展開

例として 23 を 3 進数で表すことを考えてみます。
下の図にあるように、青いブロック 1 個が数字の 1 を表すものとします。その最小単位 1 を A ブロック、3 個合わせたものを B ブロックと名づけておきます。23 を 3 で割ると 7 個の B ブロックと、2 個の A ブロックに分けられます。



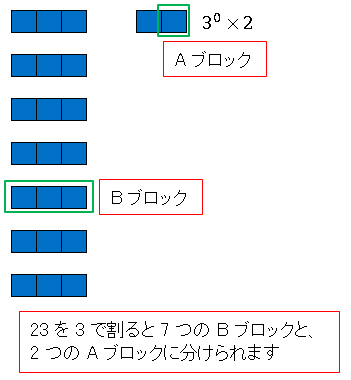
この余った 2 つの A ブロックは
\[3^0\times 2\]
と表すことができます。次に青いブロック 9 個合せたものを C ブロックと名づけます。7 を 3 で割で割ると、2 個の C ブロックと 1 個の B ブロックに分けられます。



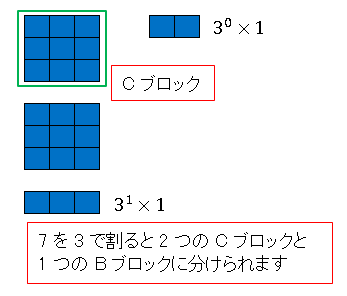
この B ブロックは
\[3^1\times 1\]
と表せます。2 は 3 で割れないので、C ブロックが取り得る最大のブロックとなります。



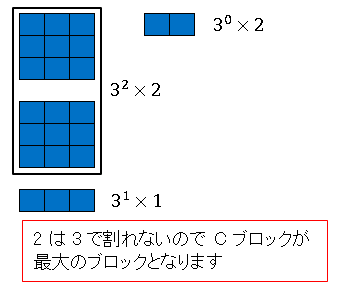
C ブロック 2 個を
\[3^2\times 2\]
と表します。したがって 23 という数字は 3 進数で
\[23=3^2\times 2+3^1\times 1+3^0\times 2\]
というように書くことができて、これを進数表示で
\[(212)_3\]
と表します。添字の 3 はこの数字が 3 進数であることを示すものです。以上の議論を一般化して整正数 $N$ を $k$ 進数で表示するために、前回学んだ 除算アルゴリズム を用います。定理 A2 を再掲しておきます。

まず整正数 $N$ を正整数 $k$ で割ります (ただし $N\gt k$ とします)。
\[N=kq_1+r_0\quad (0\leq r_0\lt k)\]
定理 A1 により、このような $q_1,\:r_0$ が唯一つ存在しています。
$q_1\geq k$ ならば、今度は $q_1$ を $k$ で割ります。
\[q_1=kq_2+r_1\quad (0\leq r_1\lt k)\]
$q_2\geq k$ ならば、今度は $q_2$ を $k$ で割ります。
\[q_2=kq_3+r_2\quad (0\leq r_2\lt k)\]
これを繰り返していくと、
\[\frac{N}{k}\geq q_1,\quad \frac{q_1}{k}\geq q_2,\quad \frac{q_2}{k}\geq q_3,\quad\cdots\]
となるので $q_n\lt k$ となるような $n$ が存在します。
\[q_{n-1}=kq_n+r_{n-1}\quad (0\lt q_n\lt k,\quad 0\leq r_{n-1}\lt k)\]
最後に $q_n$ を
\[q_n=k\cdot0+r_n\quad (0\lt r_n\lt k)\]
と表します。したがって整正数 $N$ は
\[\begin{align*}N&=kq_1+r_0\\[6pt]&=k(kq_2+r_1)+r_0\\[6pt]&=k^2q_2+kr_1+r_0\\[6pt]&=k^2(kq_3+r_2)+kr_1+r_0\\[6pt]&=k^3q_3^3+k^2r_2+kr_1+r_0\\[6pt]&=\cdots\cdots\cdots\\[6pt]&=r_nk^n+r_{n-1}k^{n-1}+\cdots+r_1k+r_0\end{align*}\]
のように表すことができます。以上をまとめると次の定理が成り立ちます。

具体的な進数変換は簡単です。たとえば 10 進数 35 を 2 進数に変換するには次のように割り算して余りを並べていくだけです。



下から数字を拾い上げて
\[(100011)_2\]
が 10 進数 35 の 2 進数表示となります。