二変数関数の極限と連続・編導関数

二変数関数

二変数関数

二変数 $(x, y)$ の組に対して $z$ の値が決まるとき、 $z$ は $x$ と $y$ の関数 (function) といい、
$z = f (x, y)$
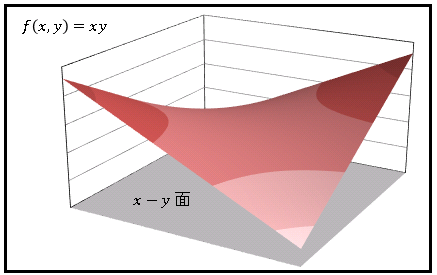
と表します。ここで $x$ と $y$ を独立変数 (independent variable)、 $z$ を従属変数 (dependent variable) といいます。独立変数 $(x, y)$ が動く範囲（ $x y$ 面上の領域）は定義域 (domain) とよばれます。定義域内の $(x, y, z)$ の集合は $x y z$ 空間における１つの曲面を表します。たとえば $z = x y$ は下図のような曲面を描きます。

Excel解析学3Dグラフz=xy

二変数関数の極限

下図のように定義域内の点 $P (x, y)$ がある点 $A (a, b)$ に近づくことを考えます。

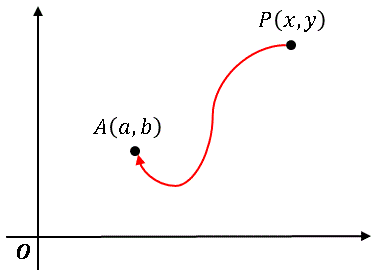
Excel2変数関数極限経路

その経路は無数にあるわけですが、どのような近づき方をしても $f (x, y)$ が同じ値 $c$ に近づく場合に限って、 $f (x, y)$ には極限が存在し、その極限値は $c$ であると定義し、次のような記号で表します。
$lim_{(x, y) \to (a, b)} f (x, y) = c$
この点 $A (a, b)$ は必ずしも定義域内に含まれているとは限らず、そのような点に対しても極限値が存在することがあります。次のような二変数の関数
$f (x, y) = \frac{x^{2}}{x^{2} + y^{2}}$
を考えます。この関数は $(0, 0)$ を除いて全平面で定義される関数です。点 $P$ が $x$ 軸に沿って原点に近づくときは
$lim_{x \to 0} f (x, 0) = lim_{x \to 0} 1 = 1$
となりますが、一方で $y$ 軸に沿って原点に近づくときには
$lim_{y \to 0} f (0, y) = lim_{y \to 0} 0 = 0$
という異なる値をとります。式だけではイメージが掴みにくいと思うので、Excel で描いた $z = f (x, y)$ の 3D グラフを載せておきます。

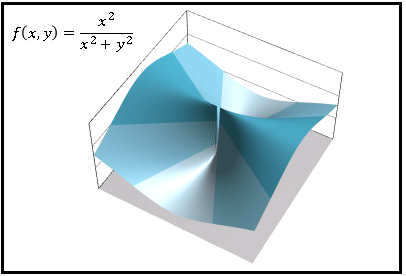
Excel解析3Dグラフ不連続点

$y$ 軸対象に２つの山があって、原点付近で尾根が細くなっています。わかりやすいように原点のところに隙間（ $z$ 軸を中心とする細い円柱空洞）を開けていますが、実際にはこの空洞の半径は無限に小さいので尾根は細い線でつながっているように見えます。 $x$ 軸に沿って極限をとるのは、この $z = 1$ の尾根に沿って原点に近づくことを意味しています。一方で $y$ 軸に沿って極限をとるときは $z = 0$ の谷に沿って空洞へ近づくので異なる値をとることになります。

二変数関数における連続の定義

二変数の関数における連続の定義を載せておきます。

点

A (a, b)

の近くで定義されている関数

z = f (x, y)

が次の条件を全て満たすとき、この関数は点

A (a, b)

で連続であるという。
①

z = f (x, y)

が定義されている。
②

lim_{(x, y) \to (a, b)} f (x, y)

が存在する。
③

lim_{(x, y) \to (a, b)} f (x, y) = f (a, b)

次のような二変数関数
$f (x, y) = {\begin{cases} \frac{x y}{x^{2} + y^{2}} & ((x, y) \neq (0, 0)) \\ 0 & ((x, y) = (0, 0)) \end{cases}$
が原点で連続であるかどうか調べてみます。最初にグラフを載せておきましょう。

Excel解析3Dグラフz=xy÷(x^2+y^2)

原点で窪んだ所があります。これは先ほどの例であげたような無限に長い円柱空洞があるわけではなく、原点付近で $z = 0$ と定義されているので、周囲と高さが著しく異なる場合があるというだけです。とくに $x y$ 平面上の直線 $y = x$ に沿った尾根とは落差が大きいですね。このことを数式で示してみましょう。まず $f (0, 0)$ は定義されているので条件 ① は満たされています。 $x$ 軸に沿って原点に近づくときは
$lim_{x \to 0} f (x, 0) = 0$
であり、また $y$ 軸に沿って原点に近づくときは
$lim_{y \to 0} f (0, y) = 0$
となっていて、極限値が存在しているかのように思えますが、直線 $y = m x (m \neq 0)$ に沿って原点に近づけてみると
$lim_{x \to 0} f (x, m x) = \frac{m}{1 + m^{2}} \neq 0$
となってしまい、やはり極限値が存在していないことがわかります。したがってこの関数は原点で連続ではありません。

偏導関数

関数 $z = f (x, y)$ において、 $y$ を固定して $x$ のみを動かしたときに
$lim_{Δ x \to 0} \frac{f (x + Δ x, y) - f (x, y)}{Δ x}$
が存在するならば、 $f (x, y)$ は変数 $x$ で 偏微分可能である といい、
$\frac{\partial f (x, y)}{\partial x}$
という記号で表します。同様に $x$ を固定して $y$ を動かしたときに
$lim_{Δ y \to 0} \frac{f (x, y + Δ y) - f (x, y)}{Δ y}$
が存在するならば、 $f (x, y)$ は変数 $y$ で 偏微分可能である といい、
$\frac{\partial f (x, y)}{\partial y}$
という記号で表します。

\begin{aligned} \frac{\partial f (x, y)}{\partial x} & = lim_{Δ x \to 0} \frac{f (x + Δ x, y) - f (x, y)}{Δ x} \\ \frac{\partial f (x, y)}{\partial y} & = lim_{Δ y \to 0} \frac{f (x, y + Δ y) - f (x, y)}{Δ y} \end{aligned}

$\partial f / \partial x, \partial f / \partial y$ のことを偏導関数（Partial derivatives）とよびます。それぞれ簡略して $f_{x}, f_{y}$ と書くこともあります。二変数の三角関数 $f (x, y) = \sin x y$ を例に、偏微分の幾何学的イメージを掴んでみます。

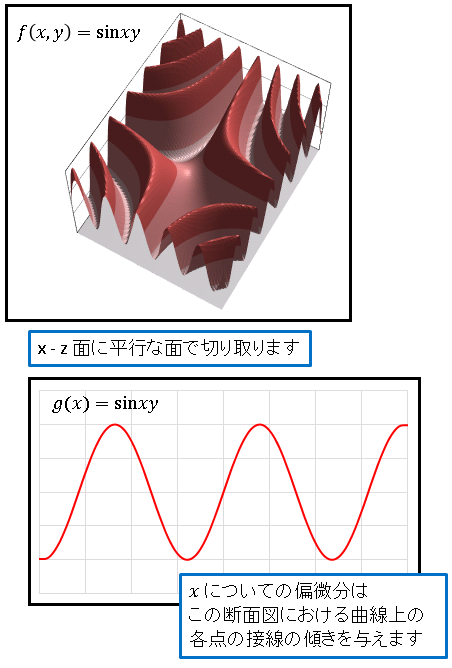
Excel3Dグラフz=sinxy

$f (x, y) = \sin x y$ は中心から四方に波が広がっていく関数です。
$y$ を固定するということは、 $x - z$ 平面に平行な面で曲面を切り取るということです。その断面図が $g (x) = \sin x y$ であり ( $y$ は定数とみているので一変数の関数です) 、これを $x$ で微分することによって $x$ 軸方向の変化率を調べることができるのです。具体的な計算は合成関数の微分公式を使って
$g^{'} (x) = f_{x} = y \cos x y$
となります。 $y$ の絶対値の大きいところでは、その周期が短くなります。理工学でよく現れるのは平面上の距離を表す関数
$r (x, y) = \sqrt{x^{2} + y^{2}}$
の偏微分です。これは少しテクニックを使います。まず両辺を平方して
$r^{2} = x^{2} + y^{2}$
それから両辺を $x$ で偏微分すると
$2 r \frac{\partial r}{\partial x} = 2 x$
となるので、
$\frac{\partial r}{\partial x} = \frac{x}{r} = \frac{x}{\sqrt{x^{2} + y^{2}}}$
というように偏導関数が求められます。 $y$ についての偏微分も同様にして
$\frac{\partial r}{\partial y} = \frac{y}{r} = \frac{y}{\sqrt{x^{2} + y^{2}}}$
となります。3 次元空間上の距離 $r (x, y, z)$ についても同じような形になるので、ぜひ試してみてください。

一変数のときと同様に、二変数関数についても高階（高次）導関数を定義することができます。1 階偏微分 $f_{x}, f_{y}$ それぞれに対して 2 種類の偏導関数が存在するので、二階偏導関数は合わせて 4 種類あります。

\begin{aligned} f_{x x} & = \frac{\partial}{\partial x} (\frac{\partial f}{\partial x}) = \frac{\partial^{2} f}{\partial x^{2}} \\ f_{x y} & = \frac{\partial}{\partial y} (\frac{\partial f}{\partial x}) = \frac{\partial^{2} f}{\partial y \partial x} \\ f_{x y} & = \frac{\partial}{\partial y} (\frac{\partial f}{\partial y}) = \frac{\partial^{2} f}{\partial y^{2}} \\ f_{y x} & = \frac{\partial}{\partial x} (\frac{\partial f}{\partial y}) = \frac{\partial^{2} f}{\partial x \partial y} \end{aligned}

$f (x, y) = x^{3} + 2 x^{2} y^{2} + 2 y^{2}$ の 2 階偏導関数を求めてみます。
$f_{x} = 3 x^{2} + 4 x y^{2}, f_{y} = 4 x^{2} y + 4 y$
なので、
$\begin{aligned} f_{x x} & = 6 x + 4 y^{2}, f_{x y} = 8 x y \\ f_{y y} & = 4 x^{2} + 4, f_{y x} = 8 x y \end{aligned}$
となります。 $f_{x y}$ と $f_{y x}$ が一致しているのは偶然ではなく、一般に $f_{x y}$ と $f_{y x}$ がともに連続ならば、偏微分の順序を変えても偏導関数が変わらないことが知られています。