sinx/xの極限値

sinx/x の極限値

　三角関数の極限値については次のような公式が知られています。
　
$$\begin{array}{}\text{(1)}& & \underset{x\to 0}{lim}\frac{\sin x}{x}=1\text{(2)}& & \underset{x\to 0}{lim}\frac{\tan x}{x}=1\text{(3)}& & \underset{x\to 0}{lim}\frac{1-\cos x}{x^2}=\frac{1}{2}\text{(4)}& & \underset{x\to 0}{lim}x\sin \frac{1}{x}=0\text{(5)}& & \underset{x\to \mathrm{\infty }}{lim}x\sin \frac{1}{x}=1\end{array}$$
　特に (1) は $\sin x$ の導関数を求めるために必要な最重要公式ですので、必ず憶えておくようにしてください。 (2) から (5) はすべて (1) から導くことができます。

証明

　(1) $f(x)=\sin x/x$ とおくと、$f(-x)=f(x)$、すなわち $f(x)$ は偶関数ですから、$x$ が正の場合について証明すればよいことになります。最終的には $x$ → $0$ の極限を考えるので、 $0<x<\pi /2$ となります。

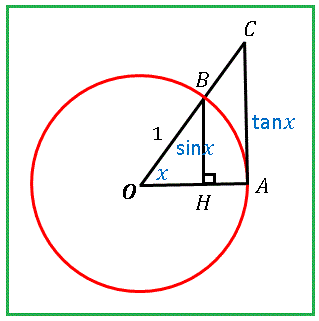
　図のように単位円と 2 つの三角形を描きます。△ OAB < 扇形 OAB < △ OAC という大小関係があります。ここで角度 $\theta$、半径 $r$ の扇形の面積は
　
$$\frac{1}{2}{r}^2\theta$$ですから、
　
$$\frac{1}{2}\sin x<\frac{1}{2}x<\frac{1}{2}\tan x$$
が成り立ちます。 $1/2$ を払って $\sin x$ で割ると
　
$$1<\frac{x}{\sin x}<\frac{1}{\cos x}$$
　逆数をとると不等号の向きが変わります。
　
$$1<\frac{\sin x}{x}<\cos x$$
　$x$ → $+0$ のとき $\cos x$ → $1$ ですから
　
$$\underset{x\to 0}{lim}\frac{\sin x}{x}=1$$
となります。

(2) の証明
　
$$\underset{x\to 0}{lim}\frac{\tan x}{x}=\underset{x\to 0}{lim}\frac{1}{\cos x}\frac{\sin x}{x}=1$$
　
(3) の証明
　
$$\underset{x\to 0}{lim}\frac{1-\cos x}{x^2}=\underset{x\to 0}{lim}\frac{1-{\cos }^{2}x}{x^2(1+\cos x)}=\frac{1}{2}$$
　
(4) の証明
　
$$\begin{gathered} 0\le \left|\sin \frac{1}{x}\right|\le 1 \\ 0\le \left|x\sin \frac{1}{x}\right|\le |x| \\ \therefore \underset{x\to 0}{lim}x\sin \frac{1}{x}=0 \end{gathered}$$
　
(5) $1/x=t$ とおくと、$x$ → $\mathrm{\infty }$ のとき $t$ → $0$ となるので
　
$$\underset{x\to \mathrm{\infty }}{lim}x\sin \frac{1}{x}=\underset{t\to 0}{lim}\frac{\sin t}{t}=1$$