【速算術】十の位と一の位に注目して掛け算します

十の位が等しく一の位の合計が10となる数同士の掛け算

タイトルの意味が分かりにくいかもしれませんが、
 

 
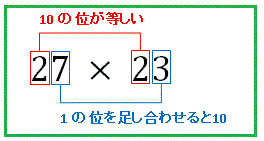
このような計算を素早く行うことを解説します。
結論から言うと、計算法は次のようになります。
 

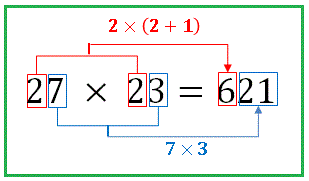
片方の数の十の位と、もう一方の数の一の位に +1 して掛け合わせて百の位とします。
一の位同士を掛け合わせて右横に書きます。
どうしてこのような計算法が成り立つのか、これまで学んできた文字式を使って説明します。二桁の数は２つの文字 $a,b$ を使って
 $$10a+b$$
と表せます。ただし、$1\le a\le 9,0\le b\le 9$ です。ちょっと試してみましょう。$a=5,b=3$ とすれば
 $$10a+b=10\times 5+3=53$$
となり、$a,b$ はそれぞれ十の位と一の位を表していることがわかります。$a,b$ にそれぞれ最小数 $1$ と $0$ を入れると、
 $$10a+b=10\times 1+0=10$$
これは二桁の数の最小数ですね。$a,b$ にそれぞれ最大の数 $9$ を入れると、
 $$10a+b=10\times 9+9=99$$
となり、二桁の数の中で最大数であることが示されました。

十の位が等しく一の位の合計が十となる二桁の数の積

冒頭で紹介したような数を一般的な式で表すにはどうしたらよいでしょうか？　とりあえず１つめの数はそのまま
 $$m=10a+b$$
とおくことにします。問題は２つめの数をどう定めるかということです。十の位は $m$ と等しいので、そのまま同じ $10a$ とします。一の位については「足して $10$」となるように、
 $$10-b$$
と書けます（$b+10-b=10$）。つまり２つめの数 $n$ は
 $$n=10a+10-b$$
と表せます。$m$ と $n$ を掛けると
 $$\begin{array}{rl}mn& =(10a+b)(10+10-b)\\ & =100a^2+100a-10ab+10ab+10b-b^2\\ & =100a^2+100a+10b-b^2\\ & =100a(a+1)+b(10-b)\end{array}$$
という式が得られます。$a(a+1)$ は「$m$ の十の位の数」と「$n$ の十の位の数に $1$ を加えた数」の積を表していますし、$b(10-b)$ は一の位の数同士の掛け算そのままです。
 
【問題】次の式を計算してください。
$(1)22\times 28(2)39\times 31(3)43\times 47$
$(4)48\times 42(5)53\times 57(6)67\times 63$
$(7)81\times 89(8)82\times 88(9)96\times 94$
 
【解答】
$(1)22\times 28=616(2)39\times 31=1209(3)43\times 47=2021$
$(4)48\times 42=2016(5)53\times 57=3021(6)67\times 63=4221$
$(7)81\times 89=7209(8)82\times 88=7216(9)96\times 94=9024$
 
次のような式に応用してみます：
 $$46\times 45$$
$46\times 44$ を思い浮かべて、次のように変形します。
 $$46\times 45=46\times (44+1)=46\times 44+46=2024+46=2070$$
数が２つずれていても何とかなります：
 $$35\times 37=35\times (35+2)=1225+70=1295$$

【問題】次の式を計算してください
$(1)29\times 22(2)52\times 59(3){26}^2$

【解答】
$(1)29\times 22=(28+1)\times 22=616+22=638$
$(2)52\times 59=52\times (58+1)=616+22=638$
$(3){26}^2=26\times (24+2)=624+52=676$

末位が5の数字の平方数

$15,25,35\cdots$ のように末位が $5$ の数を $2$ 乗するときは、この計算法が使えます：
 $$\begin{array}{rl}& {25}^2=25\times 25=625\\ & {35}^2=35\times 35=1225\\ & {45}^2=45\times 45=2025\end{array}$$
${55}^2$ から ${105}^2$ まで一気に計算してみましょう。
 
【問題】次の式を計算してください。
$(1){55}^2(2){65}^2(3){75}^2$
$(4){85}^2(5){95}^2(6){105}^2$
 
【解答】
$(1){55}^2=3025(2){65}^2=4225(3){75}^2=5625$
$(4){85}^2=7225(5){95}^2=99025(5){105}^2=11025$

十の位の合計が10で一の位が等しい数同士の掛け算

今度は次のような計算を素早く行うことを解説します。
 

 
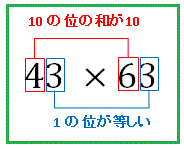
また結論から載せますが、計算法は次のようになります。
 

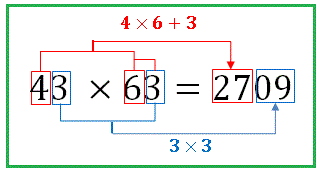
十の位同士を掛け合わせて一の位を足して百の位とします。
一の位同士をそのまま掛け合わせて右横に書きます。
 
それでは、この計算法が成り立つ理由を解説します。掛け合わせる二桁の整数 $m,n$ を一桁の整数 $a,b$ を使って次のように表します。
 $$m=10a+b,n=10(10-a)+b$$
ただし、$1\le a\le 9,0\le b\le 9$ です。$m$ と $n$ の十の位の数字 $a$ と $10-a$ は足し合わせると $10$ になっていますね。 $m$ と $n$ の積をつくると、
 $$\begin{array}{rl}mn& =\{10a+b\}\{10(10-a)+b\}\\ & =10(10a+b)(10-a)+b(10a+b)\\ & =10(100a-10a^2+10b-ab)+10ab;b^2\\ & =100a\{a(10-a)+b\}+b^2\end{array}$$
少し計算が難しいですけど、数学ではこういう計算が大切ですので、ぜひ紙に書いて練習するようにしてください。$a(10-a)+b$ は「十の位同士を掛け合わせて一の位を足す」ことを、$b^2$ は「一の位同士をそのまま掛け合わせる」ことを表しています。
 
それでは具体的な計算例を見ていきます。
 $$\begin{array}{r}19\times 96=1534\\ 33\times 73=2409\\ 65\times 45=2925\end{array}$$
冒頭の計算規則とよく見比べて確認してください。
 
【問題】次の式を計算してください
$(1)22\times 82(2)47\times 67(3)89\times 29$
$(4)35\times 75(5)49\times 51(6)94\times 14$
 
【解答】
$(1)22\times 82=1804(2)47\times 67=3149(3)89\times 29=2581$
$(4)35\times 75=2625(5)49\times 51=2499(6)94\times 14=1316$
 
公式から少しずれた場合でも工夫して応用できます：
 $$\begin{array}{r}22\times 83=22\times (82+1)=1804+22=1826\\ 47\times 68=47\times (67+1)=3149+47=3196\\ 35\times 76=35\times (75+1)=2625+35=2660\end{array}$$

十の位が5で一の位が等しい数の平方数

十の位が $5$ で一の位が等しい数字を 2 乗するときは、この計算法が使えます：
 $$\begin{array}{r}{51}^2=51\times 51=2601\\ {52}^2=52\times 52=2704\\ {53}^2=53\times 53=2809\end{array}$$
【問題】次の式を計算してください。
$(1){54}^2(2){55}^2(3){56}^2$
$(4){57}^2(5){58}^2(6){59}^2$
 
【解答】
$(1){54}^2=2916(2){55}^2=3025(3){56}^2=3136$
$(4){57}^2=3249(5){58}^2=3364(6){59}^2=3481$