直交曲線族を見つけます

直交曲線族

　$A$ を任意定数とすると $y=Ax$ は下図のような直線群となります。

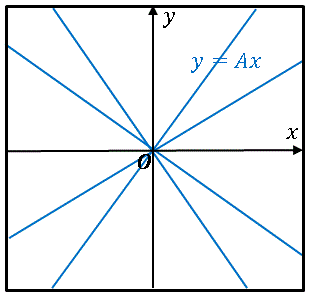
　この直線群に含まれる 全ての直線に対して直交する曲線群 を探してみます。勘の鋭い人なら上の図を見ただけで発見できるかもしれません。$y=Ax$ に直交する曲線を $y=f(x)$ とします。２つの曲線が直交するということは、交点における接線の傾きの積が －1 になるということです。$y=Ax$ の点 $(x,y)$ のおける傾きは
　
\[y’=A\]
です。求める曲線の $(x,y)$ のおける傾きを $y=f'(x)$ とすると
　
\[f’A=-1\]
　直線の方程式より $A=y/x$ なので
　
\[f’=-\frac{1}{A}=-\frac{y}{x}\]
　すなわち
　
\[\frac{dy}{dx}=-\frac{y}{x}\]
という微分方程式が得られます。変数分離すると
　
\[\int ydy=-\int xdx\]
なので
　
\[\frac{1}{2}y^2=\frac{1}{2}x^2+c\]
　$r^2=2c$ とおくと
　
\[x^2+y^2=r^2\]
という円の方程式が得られます。これは $r$ をパラメータと考えると、原点を中心とする同心円族を表しています。

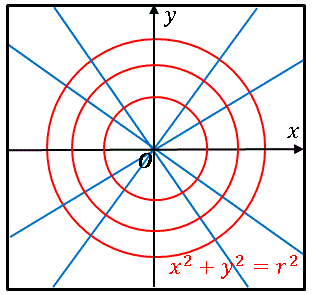
　図を見て、どの直線と円をとってきても必ず直交関係にあることを確認してください。このように与えられた曲線族すべてに直交する曲線族を 直交曲線族 とよびます。念のために上の例で、逆が成り立っているかどうか、すなわち同心円族 $y’=-x/y$ に直交する曲線族が $y=Ax$ となっているかどうか確認しておきましょう。$y’=-x/y$ に直交する曲線を $y=f(x)$ とすると、直交条件より
　
\[-f’\frac{x}{y}=-1\]
　すなわち
　
\[\frac{dy}{dx}=\frac{y}{x}\]
が成り立ちます。変数分離すると
　
\[\frac{dy}{y}=\frac{dx}{x}\]
　両辺を積分すると
　
\[\log\,|y|=\log\,|x|+c\]
　$A=\pm e^c$ とおくと
　
\[y=Ax\]
となって、確かに $A$ をパラメータとする直線群となっています。