関数の増減（極大値と極小値の判定法）

単調増加と単調減少

　関数 $f(x)$ が区間 $[a,\:b]$ で微分可能、$(a,\:b)$ で $f'(x) \gt 0$ であるとします。このとき 平均値の定理 によって
　
\[\frac{f(b)-f(a)}{b-a}=f'(c)\]
となる $c$ が存在しますが、$b=a+\Delta x$ とおくと
　
\[f(a+\Delta x)=f(a)+f'(c)\Delta x\]
と書き直せます。よって
　
\[f(a+\Delta x) \gt f(a)\]
が成り立ちます。つまり $f(x)$ は区間 $[a,\:b]$ で 単調増加 (monotonic increasing) であることがわかります。同じように $f'(x) \lt 0$ であるとき $f(x)$ は 単調減少 (monotonic decreasing) です。$f'(x)=0$ ならば $f(x)$ は 定数です。

極大値と極小値

　関数 $f(x)$ が区間 $[a,\:b]$ で連続であるとします。

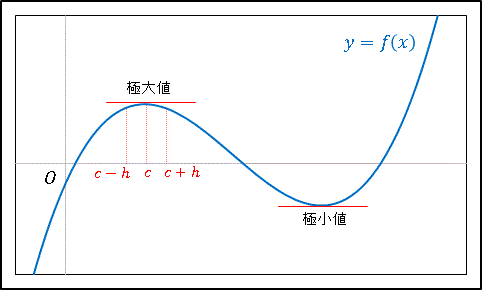
　区間内の点 $c$ において十分に小さな正数 $h$ について
　
\[f(c-h) \lt f(c),\quad f(c+h) \lt f(c)\]
が成り立つならば $f(x)$ は $x=c$ で 極大 (maximal) であるといい、$f(c)$ を 極大値 (local maximum) とよびます。同じように
　
\[f(c-h) \gt f(c),\quad f(c+h) \gt f(c)\]
が成り立つとき $f(x)$ は $x=c$ で 極小 (minimal) であるといい、$f(c)$ を 極小値 (local minimum) とよびます。極大値と極小値をまとめて極値 (extremum) とよびます。

極値をとるための必要条件と十分条件

　$f(x)$ が区間 $(a,\:b)$ で微分可能であり、区間内の点 $c$ で $f(x)$ が極大となるならば、小さな正数 $h$ に対して
　
\[\begin{align*}&\frac{f(c-h)-f(c)}{-h} \gt 0\\[6pt]&\frac{f(c+h)-f(c)}{h} \lt 0\end{align*}\]
が成立します。つまり $h\rightarrow 0$ の極限で $f'(c)=0$ が成り立ちます。同様に $f(x)$ が極小となるときも $f'(c)=0$ です。以上まとめると極値について次の必要条件がいえます。

　これはあくまで必要条件ですから逆は成立しません。たとえば $f(x)=x^3$ を微分すると $f'(x)=3x^2$ です。確かに $x=0$ で導関数は 0 になっていますが、 $f'(x)=3x^2 \geq 0$ ですから $f(x)$ は全区間で単調増加関数です。ゆえに $x=0$ で極値となってはいません。

　次は極値となるための十分条件を調べます。$f(x)$ が点 $c$ の近くで微分可能で $f'(c)=0$ とし、

　　$c \lt x$ のとき $f'(x) \geq 0$ ,　$c \gt x$ のとき $f'(x) \leq 0$

であるなら $f(x)$ は

　　$c \lt x$ のとき単調増加 ,　$c \gt x$ のとき単調減少

であるということです。つまり点 $c$ を境に減少から増加へ転じているので、$f(c)$ は極小値です。同様に

　　$c \lt x$ のとき $f'(x) \leq 0$ ,　$c \gt x$ のとき $f'(x) \geq 0$

であるなら $f(x)$ は

　　$c \lt x$ のとき単調減少 ,　$c \gt x$ のとき単調増加

となって $f(c)$ は極大値となります。以上まとめると

という極値の十分条件が得られます。

極大・極小の判定

　上の方法を使っても極値を判定することはできますが、2 階微分を使ってより簡単に判定する方法もあります。

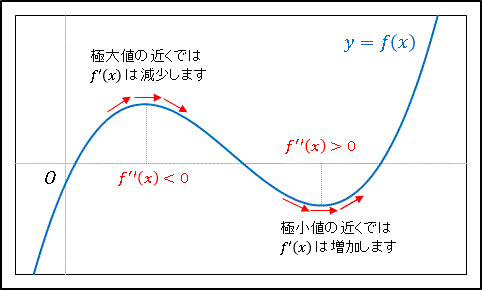
　関数 $f(x)$ が点 $c$ の近くで微分可能で $f'(c)=0$ であり、$f^{\prime\prime}(x)$ が $x=c$ を含む区間で連続であるとします。

(A) $f^{\prime\prime}(c) \lt 0$ のとき $f'(x)$ は単調減少します。$f'(c)=0$ なので、

　　　　$x \lt c$ ならば $f'(c) \gt 0$ ,　$x \gt c$ ならば $f'(c) \lt 0$

　　となります。よって、この場合 $f'(c)$ は極大値です。

(B) $f^{\prime\prime}(c) \gt 0$ のとき $f'(x)$ は単調増加します。$f'(c)=0$ なので、

　　　　$x \lt c$ ならば $f'(c) \lt 0$ ,　$x \gt c$ ならば $f'(c) \gt 0$

　　となります。よって、この場合 $f'(c)$ は極小値です。

　より直感的に捉えるなら、上の図に示したように、極大値の近くでは接線の傾きが減少し、極小値の近くでは接線の傾きが増加します。以上まとめると

となります。