たすきがけで２次式を因数分解します
今回はちょっと難しい因数分解
\[acx^2+(ad+bc)x+bd=(ax+b)(cx+d) \tag{1}\]
に挑戦します。これは たすきがけ とよばれる因数分解で、x の係数が ad + bc という交差形（後述）になっていることに由来します。
とはいえ現代では たすき なんてものを見かける機会はほとんどないでしょうから、「たすき？ 食べたことない」と思われるような若い方のために一応説明しておくと、 たすき とは和服姿の人が立ち働くときに、袖やたもとをたくし上げておくために肩から脇の下に通して背中で交差させて結ぶ紐のことです。
…… ええと、数学の話にもどりましょう。まず１度でよいので、手を動かして公式 (1) の右辺から左辺への展開を確認しておいてください。因数分解は左辺から右辺なので、４つの数 a, b, c, d を見つけるには練習が必要です。そのために使うのが下のような図です。
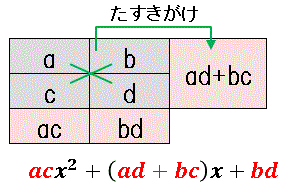
縦に掛けて x2 と定数項に一致するように、また同時にたすきがけして x の係数に一致するように a, b, c, d を探します。文字で見るだけではわかりにくいので、さっそく実例で練習しましょう。
\[6x^2+7x+2\]
という式を因数分解することを考えます。
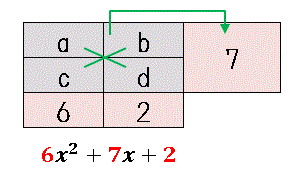
図のように係数を赤いところに入れておいて、つじつまが合うように a, b, c, d を決めていきます。適当にあたりをつけながら探します。 ac = 6 から
\[a=3,\quad b=2\]
かなあと推測してとりあえず書き留めておきます。外れたらまたあとでやり直せばよいのです。
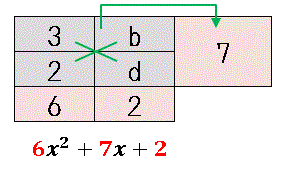
今度は bd = 2, 3d + 2b = 7 となるように b, d を決めます。
bd = 2 はどちらかが 1 でもう片方は 2 ですから２択です。
3d + 2b = 7 となるのは d = 1, b = 2 ですね。
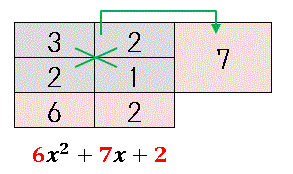
これで全てのマス目が埋まりました！
最後にもう１度つじつまが合っているかどうか確認して、
\[6x^2+7x+2=(3x+2)(2x+1)\]
と因数分解の式を書いて完了です。もちろん実際にはマス目なんて書かなくてもいいですよ。４つの数字が書き込めるようにして、下と右横に係数を書いて作業してください。繰返しトレーニングすれば頭の中でできるようになります。パズルみたいなので、子供の頃の私はたすきがけが大好きでした。でも「たすきがけが好き！」というようなことを友人には言わないほうがいいです。「変なやつ」と思われるだけです。
練習問題 因数分解してください
\((1)\:2x^2+9x+10\)
\((2)\:20x^2+29x+5\)
\((3)\:4x^2-17x+15\)
\((4)\:6x^2+7x-5\)
\((5)\:20x^2+74x+14\)
練習問題の解答
\((1)\:2x^2+9x+10=(x+2)(2x+5)\)
\((2)\:20x^2+29x+5=(5x+1)(4x+5)\)
\((3)\:4x^2-17x+15=(4x-5)(x-3)\)
\((4)\:6x^2+7x-5=(2x-1)(3x+5)\)
\((5)\:20x^2+74x+14=2(5x+1)(2x+7)\)
エクセルや数学に関するコメントをお寄せください