期待値と分散

確率密度や分布関数は完全な情報を含んでいるので、もしこれがわかっているのなら、統計的な検証など必要なくなってしまいます。しかし複雑な現実問題の多くは、このような関数がきれいな形で与えられていることは極めて稀です。とはいえ、確率密度の形はわからないけれど、とりあえず集めたデータから「分布は大体このぐらいの範囲に収まっている」というような大雑把な傾向を掴みたいときがあります。そこで活躍するのが期待値と分散です。

期待値

確率変数 $X$ の関数 $\varphi (x)$ の期待値 (expective value) を以下のように定義します。
 \[E\:[\varphi (x)]=\begin{cases}\displaystyle\sum_{i=1}^{n}\varphi (x_i)f(x_i)&\qquad (A)\\[6pt]\displaystyle\int_{-\infty}^{\infty}\varphi (x)f(x)dx&\qquad (B)\end{cases}\]
$f(x)$ は確率密度（確率関数）です。定義式 (A) は離散確率変数、(B) は連続確率変数に適用されます。特に $\varphi (x)=X^k\:(k=0,1,\cdots)$ としたときの
 \[E\:[X^k]=\begin{cases}\displaystyle\sum_{i=1}^{n}(x_i)^kf(x_i)&\qquad (C)\\[6pt]\displaystyle\int_{-\infty}^{\infty}x^kf(x)dx&\qquad (D)\end{cases}\]
を $k$ 次のモーメント (moment) とよびます。さらに 1 次のモーメント
 \[\mu=E\:[X]=\begin{cases}\displaystyle\sum_{i=1}^{n}x_if(x_i)&\qquad (E)\\[6pt]\displaystyle\int_{-\infty}^{\infty}xf(x)dx&\qquad (F)\end{cases}\]
を平均値 (mean) あるいは、$X$ の期待値（expective value）とよびます。一般によく使われる「期待値」は、この 1 次のモーメントを指します。また確率の和が 1 であるという基本性質は 0 次のモーメントとして
 \[E\:[1]=\int_{-\infty}^{\infty}f(x)dx=1\]
という形で表すことができます。

分散

平均のまわりの二次のモーメントを 分散（variance）とよびます：
 \[\sigma^2=E\:[(X-\mu)^2]=\begin{cases}\displaystyle\sum_{i=1}^{n}(x_i-\mu)^2f(x_i)&\qquad (G)\\[6pt]\displaystyle\int_{-\infty}^{\infty}(x-\mu)^2f(x)dx&\qquad (H)\end{cases}\]
また、分散は平均値 $\mu$ を用いて
 \[\begin{align*}\sigma^2&=E\:[(X-\mu)^2]\\[6pt]&=\int_{-\infty}^{\infty}(x^2-2\mu x+\mu^2)f(x)dx\\[6pt]&=E\:[X^2]-2\mu E\:[X]+\mu^2E\:[1]\\[6pt]&=E\:[X^2]-2\mu^2+\mu^2=E\:[X^2]-\mu^2\end{align*}\]
と表すこともできます：
 \[\sigma^2=E\:[X^2]-\mu^2\]
分散 $\sigma^2$ の平方根をとった $\sigma$ を 標準偏差 (standard deviation) といいます。定義からわかるように、分散や標準偏差はある確率変数が平均値から離れているほど値が大きくなり、データのばらつき具合の指標になっています。
 

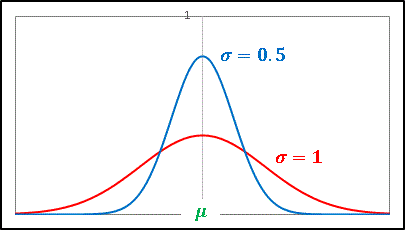
上の図は正規分布における $\sigma=0.5$ と $\sigma=1$ のグラフです。このように $\sigma$ の値が大きいほど曲線の幅が広がります。

期待値と分散の計算例

離散確率変数

サイコロを 1 回振って出た目の変数を $X$ とします。確率密度は $f(x_i)=1/6\:(i=1,2,\cdots,6)$ なので、期待値（平均値）は
 \[\mu=E\:[X]=\sum_{i=1}^{6}x_if(x_i)=\frac{7}{2}=3.5\]
で与えられます。これはサイコロを繰り返し振ったときに「出る目の平均が 3.5」であることを意味しています。実際にサイコロを 100 回投げて、出た目を全て足して 100 で割れば、おおよそ 3.5 の値になるということです。$\mu$ が得られたので、それを用いて $X$ の分散を計算すると
 \[\sigma^2=(1-3.5)^2\times\frac{1}{6}+(2-3.5)^2\times\frac{1}{6}+\cdots+(6-3.5)^2\times\frac{1}{6}=2.92\]
また標準偏差は $\sigma=\sqrt{2.92}=1.71$ となります。

連続的確率変数

確率統計分野でよく使用されるガンマ関数は
 \[\Gamma (x)=\int_{0}^{\infty}t^{x-1}e^{-t}dt\]
という積分で定義され、$x$ が整数のときは
 \[\Gamma (n+1)=n!\]
のように簡単に計算できます。これを用いて
 \[\begin{align*}&\int_{0}^{\infty}te^{-t}dt=\Gamma (2)=1!=1\\[6pt]&\int_{0}^{\infty}t^{2}e^{-t}dt=\Gamma (3)=2!=2\\[6pt]&\int_{0}^{\infty}t^{3}e^{-t}dt=\Gamma (4)=3!=6\end{align*}\]
という積分値を準備しておきます。
 \[f(x)=\begin{cases}xe^{-x} & (x\geq 0)\\[6pt]0 & (x\lt 0)\end{cases}\]
で与えられるような分布を考えてみます。まず $f(x)$ を全区間で積分した値（確率の和）が 1 となることを確認しておきましょう。
 \[\int_{-\infty}^{\infty}f(x)dx=\int_{0}^{\infty}xe^{-x}dx=1\]
また期待値を計算すると
 \[\mu=E\:[X]=\int_{-\infty}^{\infty}f(x)dx=\int_{0}^{\infty}x^2e^{-x}dx=2\]
となります。下図のように期待値を境目として $0\leq x\leq 2$ と $2\leq x$ の面積は同じになっています。
 

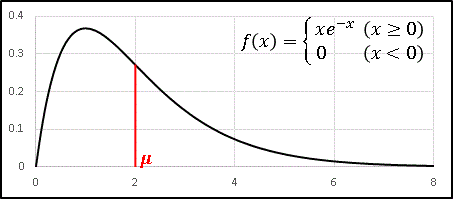
分散は次のように計算できます。
 \[\begin{align*}\sigma^2&=\int_{0}^{\infty}(x-2)^2xe^{-x}dx\\[6pt]&=\int_{0}^{\infty}(x^3-4x^2+4x)e^{-x}dx\\[6pt]&=\Gamma (4)-4\Gamma (3)+4\Gamma (2)=2\end{align*}\]
標準偏差は分散の平方根をとって $\sigma=\sqrt{2}=1.414$ となります。