Excel には円周率を求める PI関数 が用意されていますが、VBA にはそれらしきものが見当たらないので「何でこんな基本的な関数がないの???」と面食らってしまうかもしれません。でも心配御無用です。VBA には逆正接を返す Atn という関数が用意されていて、ちゃんと円周率が使えるようになっています。 WorksheetFunction でワークシート関数 PI を呼び出す必要はありません。
結論から言うと、Atn(1) の 4 倍が円周率πに相当します。すなわちコードの中で pi を Double 型として宣言しておいて
Dim pi As Double pi = 4*Atn(1)
と書いておけば変数 pi を円周率として使うことができます。これさえ知っていれば、コードを書く上で困ることはありませんが、もう少し数学的背景を知りたい人のために逆正接関数について要点を絞って説明しておきます。
高校数学で三角関数 sin, cos, tan などを学びますが、それらの逆関数として逆三角関数というものが存在します。逆三角関数一般の詳しい解説は他のページに譲るとして、ここでは、その中の Arctan に限定して簡単に説明します。tan と Arctan は次のような関係になっています。
y = tanx ⇔ x = Arctan(y)
具体的な数値を入れるとイメージしやすくなります。
下図のように直角を挟む二辺の長さが等しい三角形を作ります。
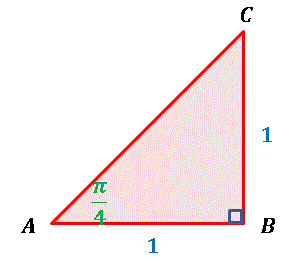
∠A = π/4 ですから、斜辺の傾きは 1 となりますね。これを三角関数で表すと
1 = tan(π/4) ⇔ π/4 = Arctan(1)
となります。つまり傾きが 1 になるような角度が Arctan(1) ということです。このように逆三角関数の戻り値は常に「角度」となります。上の式から Arctan(1) を 4 倍すれば円周率が得られます。
VBA の簡単なプロシージャで円周率の精度を確認しておきましょう。
'[VBA] 円周率の計算 Sub PI_TEST() Dim pi As Double pi = 4 * Atn(1) Debug.Print pi End Sub
PI_TEST() を実行するとイミディエイトウィンドウに 3.14159265358979 という有効数字 15 桁の円周率が表示されます。これはワークシート関数の PI と同じ精度です。
1 ラジアンすなわち 180/π を計算するマクロです。
'[VBA] 1ラジアンの計算 Sub ONE_RADIAN() Dim pi As Double, rad As Double pi = 4 * Atn(1) rad = pi / 180 Debug.Print rad End Sub
pi = 4 * Atn(1) で円周率を定義して、その値を 180 で割っています。ONE_RADIAN() を実行するとイミディエイトウィンドウに 57.295 … という有効数字 15 桁の数字が表示されます。
引数に半径を指定すると球の体積を返すファンクションマクロ(ユーザー定義関数)を載せておきます。
'[VBA] 球の体積の計算 Function V_Sphere(radius As Double) As Double Dim pi As Double pi = 4 * Atn(1) V_Sphere = 4 * pi * radius ^ 3 / 3 End Function
シート上で「=V_Sphere(1)」と入力すると 4.188 … (半径 1 の球の体積) を返します。

エクセルや数学に関するコメントをお寄せください