【VBA】二次方程式の係数を漸化式で定めます

2次方程式の係数を漸化式で定めます

ふとした思いつきで、こんなことを試してみました。
\[z^2+a_{n+1}z+a_n=0\]
という二次方程式を考え、係数 $a_{n+1}$ と $a_n$ は漸化式によって値を定めて、その解を複素平面上に描いてみようという試みです。漸化式の形は色々と試してみたのですが、その中のひとつ
\[a_{n+1}=\frac{a_n+1}{n},\quad a_0=2\]
のグラフを紹介します。すなわち
\[\begin{align*}&z^2+3z+2=0\\[6pt]&z^2+2z+3=0\\[6pt]&z^2+z+2=0\\[6pt]\end{align*}\]
という方程式を次々と解かせて、その解を複素平面上にプロットしていきます。解を求めるコードは以下のようになります。

'[VBA] 係数を漸化式で定める二次方程式

Sub Recurrence_Coefficient()

　　Dim an0 As Double
　　Dim an1 As Double
　　Dim d As Double
　　Dim k As Integer

　　'初期値a0の設定
　　an0 = 2
　　y1 = 0
　　y2 = 0

　　For k = 1 To 100
　　　　'漸化式によって係数を定める
　　　　an1 = (an0 + 1) / k

　　　　'判別式の計算
　　　　d = an1 ^ 2 - 4 * an0

　　　　'判別式が0以上なら実数解
　　　　If d >= 0 Then
　　　　　　x1 = (-an1 + Sqr(d)) / 2
　　　　　　x2 = (-an1 - Sqr(d)) / 2
　　　　'そうでなければ虚数解
　　　　Else
　　　　　　'実部の計算
　　　　　　x1 = -an1 / 2
　　　　　　x2 = x1
　　　　　　'虚部の計算
　　　　　　y1 = Sqr(Abs(d))
　　　　　　y2 = -Sqr(Abs(d))
　　　　End If

　　　　'nと二解の実部と虚部を並べる 
　　　　Cells(k, 1) = k
　　　　Cells(k, 2) = x1
　　　　Cells(k, 3) = y1
　　　　Cells(k, 4) = x2
　　　　Cells(k, 5) = y2

　　　　an0 = an1

　　Next k

End Sub

Recurrence_Coefficient() を実行すると、A 列に $n$, B 列と C 列に一方の解の実部 $\mathrm{Re}z_1$ と虚部 $\mathrm{Im}z_1$, D 列と E 列に他方の解の実部 $\mathrm{Re}z_2$ と虚部 $\mathrm{Im}z_2$ が出力されます。

$(\mathrm{Re}z_1,\:\mathrm{Im}z_1)$ を一組のデータ、また $(\mathrm{Re}z_2,\:\mathrm{Im}z_2)$ をもう一組のデータとして散布図を描くと次のようになります (A 列のデータは使いません)。



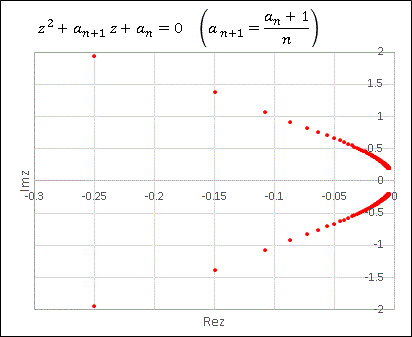
2 解が $x$ 軸に関して対称にペアを作りながら曲線を描きます。$n$ が大きくなると (－0.005, 0.2), (－0.005, －0.2) という値に収束していく様子がわかります。漸化式の部分を変えれば曲線の形も変わります。皆さんも色々と試して面白いグラフを探してみてください。