【VBA】数学練習問題
VBA を使って解く数学の練習問題を用意しました。ぜひチャレンジしてください。
【VBA練習問題01】トリボナッチ数列 (Tribonacci Sequence)
次のように、ある項が前の $3$ 項の和で定義される数列
\[\begin{align*}&T_0=0,\quad T_1=0,\quad T_2=1\\[6pt]&T_{n+3}=T_{n+2}+T_{n+1}+T_{n}\quad (n\geq 0)\end{align*}\]
をトリボナッチ数列 (Tribonacci Sequence) とよびます。この数列の初項 $T_0$ から $15$ 番目の項 $T_{14}$ までを表示させる Subプロシージャ (Subroutine) を記述してください。
【ヒント】数列を扱うコードは配列と相性がいいです。
問題文では $T_n$ の初項を $T_0$ としているので、配列の下限値を設定する Option Base は 0 のままがよいでしょう（デフォルトで 0 になっているので、宣言セクションには何も書く必要はありません）。本問に限りませんが、実行結果は MsgBox で表示するよりも Debug.Print (Debugオブジェクトの Printメソッド) を使った方が便利です（イミディエイトウィンドウで実行結果を確認しながらコードを修正できます）。
【解答】次のような手順で処理を実行します。
・トリボナッチ数列の各項を入れるために、Dim ステートメントで 15 個の要素からなる配列変数を宣言します。
・t(0), t(1), t(2) には数列の初期値 $T_0$, $T_1$, $T_2$ の値を入れます。
・フィボナッチ数列の漸化式
\[T_{n+3}=T_{n+2}+T_{n+1}+T_{n}\quad (n\geq 0)\]を配列を使って
t(k) = t(k - 1) + t(k - 2) + t(k - 3)
と表し、変数 k を 3 から 14 まで動かしながら、配列に値を代入していきます。解答コードは次のようになります。
'[VBA練習問題1]トリボナッチ数列 (Tribonacci Sequence)
Sub Tribonacci()
'ループ処理に用いる変数を長整数型で宣言
Dim k As Long
'15 個の要素からなる配列を長整数型で宣言
Dim t(14) As Long
'初期値の代入
t(0) = 0
t(1) = 0
t(2) = 1
't(3)～t(14) の計算
For k = 3 To 14
t(k) = t(k - 1) + t(k - 2) + t(k - 3)
Next k
't(0)～t(14) の表示
For k = 0 To 14
Debug.Print "T(" & k & ") = " & t(k)
Next k
End Sub
'実行結果：
'T(0) = 0
'T(1) = 0
'T(2) = 1
'T(3) = 1
'T(4) = 2
'T(5) = 4
'T(6) = 7
'T(7) = 13
'T(8) = 24
'T(9) = 44
'T(10) = 81
'T(11) = 149
'T(12) = 274
'T(13) = 504
'T(14) = 927
k ≥ 3 では T(k) が前 3 項の和になっていることを確認しておいてください。
たとえば、T(6) = 7, T(7) = 13, T(8) = 24 なので、
T(9) = T(8) + T(7) + t(6) = 44
となっています。
【VBA練習問題02】バクテリアの増殖
1 時間ごとに分裂して個数が 2 倍になるバクテリアがあります。このバクテリアが最初 (時刻 t = 0) に 1 個存在したとして、1 億個を超えるときの時間 t と、そのときのバクテリアの個数 n を出力するコードを書いてください。
【ヒント】
・ある数を超えるまでという問題に適したループ処理の方法があります。
・個数は 2t を計算させるのではなく、再帰という方法で処理してみましょう。
【解答】時間とバクテリアの個数をそれぞれ t, n で表し、初期値は 0, 1 とします。
Do Until … Loop ステートメントを使って、n が 108 を超えるまで、
t に 1 を加え、n は 2 倍する
という処理を繰り返します（あるいは Do While … Loop を使います）。
'[VBA練習問題02]バクテリアの増殖プログラム Sub Bacteria() Dim n As Long Dim t As Long '個数の初期値 n = 1 '時刻の初期値 t = 0 Do Until n > 10 ^ 8 '時間に 1 を加える t = t + 1 '個体数を 2 倍にする n = n * 2 Loop Debug.Print "t = " & t Debug.Print "n = " & n End Sub '実行結果： 't = 27 'n = 134217728
という結果が表示されます。すなわち、バクテリアは 27 時間後に 134,217,728 個に増殖します。
【VBA練習問題03】11 もしくは 19 で割り切れる数
100 以下の自然数のうち、11 もしくは 19 で割り切れる数を列挙して、それらの数字の合計値を表示するプログラムを書いてください。
【ヒント】ループ処理の中に条件分枝を入れる典型的なアルゴリズムです。If文には「11 で割り切れる」または「19 で割り切れる」という条件式を記述します。
【解答】[1] 判定する数を k, 総和を s とします。
[2] それぞれの初期値は k = 1, s = 0 に設定しておきます。
[3] k が条件を満たす場合は、その値を表示して s に k を加えます。条件を満たさなければ何もしません。
[4] k に 1 を加えます。
[5] [3] と [4] を繰り返し、k が 101 に達したらループを止めます。
[6] 総和 s の値を表示します。
'[VBA練習問題03]11 もしくは 19 で割り切れる数の探索 Sub Divisible() Dim k As Long, s As Long ' k（判定する数）の初期値 k = 1 ' s (総和) の初期値 s = 0 ' k が 101 に達するまでループ Do While k < 101 '「11 で割り切れる」または「19 で割り切れる」場合 If (k Mod 11 = 0) Or (k Mod 19 = 0) Then ' 条件を満たす数を表示 Debug.Print k; s = s + k End If k = k + 1 Loop ' 条件を満たす数の総和を表示 Debug.Print "S = " & s End Sub ' 実行結果： ' 11 19 22 33 38 44 55 57 66 76 77 88 95 99 ' S = 780
という結果が表示されます。Debug.Print で k の値を表示させるところでセミコロン「 ; 」を添えていますが、これは数字を横並びに表示させるオプションです。細かいテクニックですが、覚えておくと結構便利です。
【VBA練習問題04】三角数を判定するプログラム
下図のように正三角形の形に点を並べたときに、そこに並ぶ点の総数を三角数 (triangular number) とよびます。
$n$ 番目の三角数を $T(n)$ とすると、
\[\begin{align*}&T(1) = 1\\[6pt]&T(2) = 1 + 2 = 3\\[6pt]&T(3) = 1 + 2 + 3 = 6\\[6pt]&T(4) = 1 + 2 + 3 + 4 = 10\\[6pt]&\cdots\cdots\cdots\cdots\cdots\cdots\\[6pt]&T(n)=\frac{n(n+1)}{2}\end{align*}\]
と表すことができます。
(1) 任意の整数を引数に渡して、それが三角数であれば True、そうでなければ False を返す Functionプロシージャ（ユーザー定義関数）を作ってください。関数の名前は Triangular とします。
(2) Triangular関数を使って、785631 が三角数であるかどうかを判定してください。
【ヒント】コードを書く前に「三角数であることを判定する方法」を見つける必要があります（これは純粋に数学の問題です）。
【解答】(1) 与えられた自然数 $x$ が三角数であるとき、
\[x=\cfrac{n(n+1)}{2}\]
となります。$n$ について整理すると
\[n^2+n-2x=0\]
という $n$ の 2 次方程式が得られます。解の公式を使ってこの方程式を解くと
\[n=\frac{-1+\sqrt{1+8x}}{2}\]
となります (2 解のうち正の値をもつ解だけが意味をもちます)。$n$ が自然数ならば $x$ は三角数 $T(n)$ です。$n$ が自然数でなければ $x$ は三角数ではありません。すなわち
\[d=\frac{-1+\sqrt{1+8x)}}{2}\]
が $x$ が三角数であるか否かの判定式となります。
'[VBA練習問題04]三角数判定関数 Function Triangular(x As Long) As Boolean Dim d As Double '三角数の判定式 d = (-1 + Sqr(1 + 8 * x)) / 2 'd が整数かつ 0 でない場合 If d = Int(d) And d <> 0 Then Triangular = True Else Triangular = False End If End Function
Triangular関数の引数には整数型を渡すようにします。関数の戻り値は何も書かなければ Variant になるので、それでも構いませんが、解答例では真偽値を返す関数であることを明示するために Boolean型にしてあります。判定式 d が整数であることは
d = Int(d)
が成り立つことと同値です (Int()は数値の整数部を取得する関数です)。d が 0 のときも (n = 0 となるので) 条件を満たさないことに注意してください。
(2) ワークシートのセルに
=Triangular(785631)
と入力するか、次のマクロ
Sub Test_Triangular() Debug.Print Triangular(785631) End Sub
を実行すると True が返るので、785631 は三角数です。
【VBA練習問題05】円柱の表面積と体積を返す関数
(1) 底面半径 r と高さ h を渡すと円柱の表面積と体積を返す Functionプロシージャ（ユーザー定義関数）を作ってください。関数名は Cylinder とします。
(2) Cylinder関数を使って、底面の半径が 15, 高さが 80 の円柱の表面積と体積を求めてください。
【ヒント】・底面半径 $r$, 高さ $h$ の円柱の表面積 $S$ と体積 $V$ は次式で与えられます。
\[\begin{align*}&S=2\pi(r^2+rh)\\[6pt]&V=\pi r^2 h\end{align*}\]
・円周率の値が必要です。定数 3.141592654 … を定義してもいいですし、他にも 逆正接関数を使った方法 があります。
・Cylinder関数は 2 つの値を返さなくてはなりません。複数のデータをまとめて扱うときにはユーザー定義型変数（構造体）を用います。構造体については Excel VBA 表計算とプログラミング教室 というサイトに詳しい説明があるので参照してください。
【解答】コードの概要は以下のようになります。
[1] Cylinder関数は表面積と体積の 2 種類の値を返すので、宣言セクションで Type ステートメントを使ってユーザー定義型変数を宣言しておきます。解答コードでは、Solid 型という名前で宣言し、表面積と体積を格納する変数はそれぞれ sarea, volume という名前にしています。
[2] Cylinder関数の戻り値を Solid 型にします。
[3] 円周率を定義します。解答コードでは 4 * Atn(1) で定義しています。
[4] Cylinder関数の sarea変数に表面積を入れるようにします。
[5] Cylinder関数の volume変数に体積を入れるようにします。
'[VBA]Solid Figure (立体図形) の変数
Type Solid
'表面積を格納する変数
sarea As Double
'体積を格納する変数
volume As Double
End Type
'円柱の表面積と体積を計算する Functionマクロ
Function Cylinder(r As Double, h As Double) As Solid
Dim pi As Double
'円周率の定義
pi = 4 * Atn(1)
'表面積の計算
Cylinder.sarea = 2 * pi * (r ^ 2 + r * h)
'体積の計算
Cylinder.volume = pi * r ^ 2 * h
End Function
(2) 次のようなサブルーチンを作って関数を呼び出します。
Sub Test_Cylinder() Debug.Print "S = " & Cylinder(15, 80).sarea Debug.Print "V = " & Cylinder(15, 80).volume End Sub '実行結果： 'S = 8953.53906273091 'V = 56548.6677646163
【VBA練習問題06】関数の最大値の判定
(1) 関数 f(n) = an2 + bn + c (a, b, c は実数) において、n が整数値 －s, …, 0, 1, 2, … s をとるとき、f(n) を最大にする n と、そのときの f(n) の値を返す Functionプロシージャ（ユーザー定義関数）を作成してください。この関数の名前は NQuad とし、a, b, c, s は引数で指定するものとします。
(2) f(n) = －n2 + 15n + 6 において、n が整数値 －10, …, 0, 1, 2, … 10 をとるとき、f(n) を最大にする n と、そのときの f(n) の値を求めてください。
【ヒント】NQuad関数は 2 つの値を返さなくてはなりませんし、f(n) を最大にする n は Long あるいは Integer, 最大値のほうは Double で宣言する必要があります。このように異なる型の複数のデータをまとめて扱うときにはユーザー定義型変数（構造体）を用います。構造体については Excel VBA 表計算とプログラミング学習サイト に詳しい説明があるので参照してください。
【解答(1)】宣言セクションで Typeステートメントを使って、f(n) が最大となる変数を入れる nmax を Long型で、最大値を入れる変数 fmax を Double型で宣言しておきます。NQuad関数は次のようなアルゴリズムで作成します。
[1] n = 0 の 1 点だけを考えると、最大値をとる n は nm = 0 であり、最大値は fm = f(0) = c となります。
[2] k = －s とします。f(－s) が f(0) より大きければ nm を －s に、fm を f(－s) で置き換えます。そうでなければ nm, fm はそのまま据え置きます。k に 1 を加えます。
[3] k = －s とします。f(－s + 1) が f(－s) より大きければ nm を －s + 1 に、fm を f(－s + 1) で置き換えます。そうでなければ nm, fm はそのまま据え置きます。k に 1 を加えます。
[4] [2] と [3] を k = s になるまで繰り返します。
[5] NQuad.nmax に nm を、NQuad.fmax に fm を入れます。
'[VBA]最大値をとるnと、最大値f(n)を格納する変数 Type Maxdata nmax As Long fmax As Double End Type 'f(n)=an2+bn+cの最大値をとるnと、最大値f(n)を求める関数 Function NQuad(a As Double, b As Double, c As Double, s As Long) As Maxdata Dim k As Long Dim nm As Long Dim fm As Double Dim func As Double 'f(n) が最大となる n の初期値 nm = 0 '最大値 f(m) の初期値 fm = c For k = -s To s func = a * k ^ 2 + b * k + c 'funcがfmより大きければ If func > fm Then 'f(n)が最大値となるnを置き換える nm = k '最大値f(m)を置き換える fm = func End If Next k NQuad.nmax = nm NQuad.fmax = fm End Function
【解答(2)】NQuad関数の引数に、a = －1, b = 15, c = 6, s = 10 を入れて呼び出します。
Sub NQuadTest() Debug.Print "nmax = " & NQuad(-1, 15, 6, 10).nmax Debug.Print "f(nmax) = " & NQuad(-1, 15, 6, 10).fmax End Sub '実行結果： 'nmax = 7 'f(nmax) = 62
【VBA練習問題07】0 から 9 がランダムに並ぶ数列
$a_0$ と $a_1$ は $0$ から $9$ のランダムな数をとるものとし、$a_3$ 以降は次のような規則で項を作るものとします。
・前の $2$ 項を足し合わせて $9$ を超えなければ、足した数字を新しい項とします。
・前の $2$ 項を足し合わせて $9$ を超えたときは、足した数字の一の位を新しい項とします。
このような規則で作られる数列を初項から $10$ 項並べるプロシージャをつくってください。
【ヒント】
・0 ～ 1 の乱数は Rnd関数で得られますが、この関数を上手く利用して 0 ～ 9 の整数の乱数をつくります。
・一の位の数字を取得する方法を考えましょう。
【解答】[1] 10 個の要素をもつ配列 a(9) を宣言します
[2] Randomizeステートメントで乱数ジェネレータを初期化します
[3] Rndは 0 以上 1 未満の乱数を生成するジェネレータです。
a, b を整数 (a < b) とするとき、a ～ b の一様乱数を生成する場合は
Int((b - a + 1) * Rnd + a)
と記述します。a(0) と a(1) には 0 ～ 9 の乱数を入れるので、a = 0, b = 9 として
a(0) = Int(10 * Rnd) a(1) = Int(10 * Rnd)
と記述します。
[4] a(1) を a(2) を加えて 9 を超えない場合は、その値を a(3) とします。
9 を超える場合は a(1) + a(2) を 10 で割った余りを a(3) とします。
[5] [4] と同じようにして、a(4), a(5), …… a(9) をつくります。
'[VBA]初期値がランダムに決まる数列 Sub Random_Sequence() Dim k As Long '10個の要素をもつ配列を定義 Dim a(9) As Long '乱数ジェネレータの初期化 Randomize '1～9の整数乱数 a(0) = Int(10 * Rnd) a(1) = Int(10 * Rnd) 'a(2)～a(9)を生成 For k = 2 To 9 a(k) = a(k - 1) + a(k - 2) 'a(k)が10 以上の場合 If a(k) > 9 Then 'a(k)を10で割った余り a(k) = a(k) Mod 10 End If Next k 'a(k)を並べて表示 For k = 0 To 9 Debug.Print a(k); Next k End Sub '実行結果： '2 7 9 6 5 1 6 7 3 0
【VBA練習問題08】正方形状に 1 ～ n の数字を並べます
ユーザーが任意の数字 n を入力すると、ワークシートに 1 ～ n2 の数字が正方形状に並ぶようなマクロをつくってください。最初の数字 (1) はセル A1 に入るものとします。たとえば、n = 5 の場合は次のように数字が並びます。
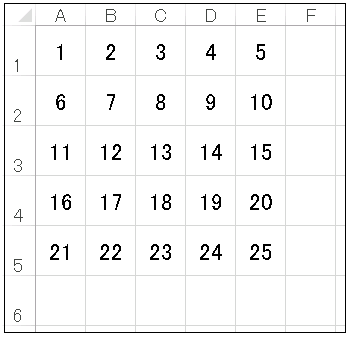
【ヒント】
・ユーザーが n を入力できるようにします。
・ループでセルを処理するときは Cellsプロパティを使います。
・Cells(y, x) は y 行 x 列のセルを意味します。
・2 つの変数を使って二重ループさせます。
【解答】Cells(k, j) は k 行 j 列のセルを取得します。下図のように、n = 5 のとき、A 列には初項 1, 公差 5 の等差数列が並ぶので、Cells(k, 1) に入る数字は
1 + 5 (k - 1) = 5 k - 4
と表せます。k 行には初項 5 k – 4, 公差 1 の数列が並ぶので、Cells(k, j) には、
5 k - 4 + j
という数字が入ることになります。
一般の n について考えると、A 列には初項 1, 公差 n の等差数列が並ぶので、Cells(k, 1) は
1 + n (k - 1)
と表せます。k 行には初項 n (k – 1) + 1, 公差 1 の数列が並ぶので、Cells(k, j) は、
n (k - 1) + 1 + j - 1 = n (k - 1) + j
と表せます。
'[VBA]数字を正方形状に並べるマクロ
Sub Fill_Square()
Dim k As Long, j As Long, n As Long
'ユーザーが n を入力
n = InputBox("nを入力")
For k = 1 To n
For j = 1 To n
Cells(k, j) = n * (k - 1) + j
Next j
Next k
End Sub
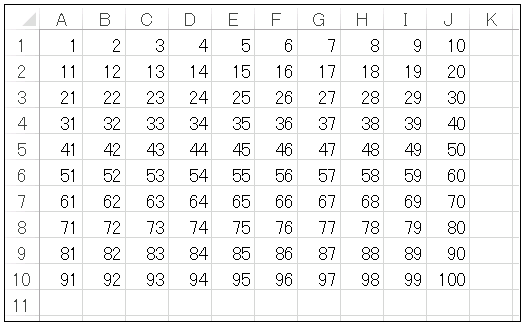
n = 10 で Fill_Square() を実行すると下図のように 100 個の数字が並びます。
エクセルや数学に関するコメントをお寄せください