【VBA】二分法のアルゴリズム

この記事では二分法の原理と、VBA で二分法を実装する方法について解説します。

【VBA】二分法で方程式の近似解を求める

方程式 $f(x)=0$ について、適当な初期値 $a,\:b\:(a\lt b)$ を与えます。このとき
\[f(a)\lt 0,\quad f(b)\gt 0\]
であるとすると、方程式 $f(x)=0$ の解は $a$ と $b$ の間にあることがわかります。

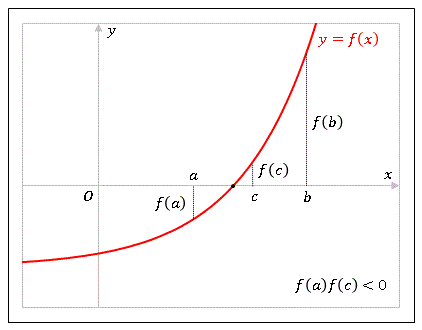
そこで、$a$ と $b$ の中点
\[f(c)=\frac{a+b}{2}\]
を求めて $f(c)$ の符号を調べます。このとき、
\[f(a)f(c)\lt 0\]
ならば、$b$ と $c$ の間に解があります。そして中点 $c$ をあらためて $b$ とおきます。

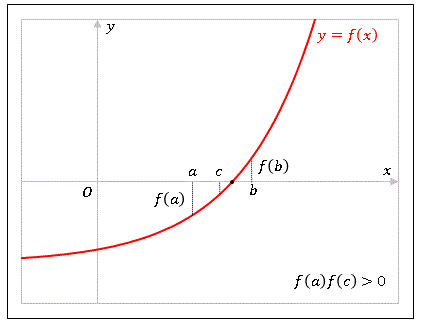
再び $a$ と $b$ の中点 $c$ について $f(c)$ の符号を調べて、今度は
\[f(a)f(c)\gt 0\]
であったとすると、解は $a$ と $c$ の間にあることになります。このように二分割を繰り返して解が存在する区間を小さくしていくことで、$c$ を真の解に近づけていくことができます。この方法を 二分法 (Bisection method) とよびます。

VBA に二分法を実装して、$x^2=2$ の解を求めてみましょう。つまり $\sqrt{2}$ の近似値を計算させることになります。解の含まれる区間 $b-a$ があらかじめ設定した収束判定定数 EPS 以下になったときに計算を打ち切って、そのときの $c$ を近似解とします。

'[VBA]二分法でx^2=2の解を求めるプログラム

'f(x)=x^2-2
Function My_Function(x As Double) As Double
　　My_Function = x ^ 2 - 2
End Function

'二分法でx^2-2=0の解を求めるサブルーチン
Sub Bisection()

　　Dim a As Double, b As Double, c As Double
　　Dim f1 As Double, f2 As Double
　　Dim eps As Double, k As Integer

　　eps = 0.001

　　a = InputBox("初期値 a を入力してください")
　　b = InputBox("初期値 b を入力してください")

　　f1 = My_Function(a)
　　f2 = My_Function(b)

　　If f1 * f2 > 0 Then
　　　　Debug.Print "この区間には解が含まれないか複数存在する可能性があります"
　　　　Debug.Print "区間を入力し直してください"
　　　　Exit Sub
　　End If

　　Do While Abs(b - a) > eps And k < 100
　　　　k = k + 1
　　　　c = (a + b) / 2
　　　　f1 = My_Function(a)
　　　　f2 = My_Function(c)
　　　　If f1 * f2 < 0 Then
　　　　　　b = c
　　　　Else
　　　　　　a = c
　　　　End If
　　Loop

　　Debug.Print c

End Sub

Bisection() を実行すると a と b の入力が促されます。たとえば a = 3, b = 0 を入力すると 1.412109… という値が表示されるはずです（真値は 1.4142135 … ）。eps の値を小さくすれば、より高い精度の近似解を返します。My_Function の中身を別の関数に書き換えることで、色々な方程式の近似解を計算することができるので、ぜひ試してみてください。