道順問題（最短距離で目的地に達する道順の総数）

道順の個数

図のように東西 4 条、南北 6 条で区画された市街地があります。
 

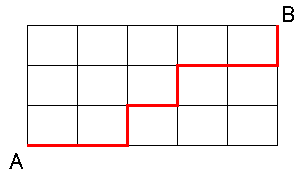
A 地点から出発してから B 地点に最短距離で到達する道順が何通りあるのか考えてみましょう。上図の赤い線は道順の 1 例です。1 回通った道を引き返さない限り、どこを通っても最短距離となります。そこで横方向への移動を X , 縦方向の移動を Y という記号で書くことにすれば、図の赤い線は「X X Y X Y X X Y」というように表すことができます。どのような道順であっても X の総数は 5 , Y の総数は 3 となっています。
 
つまり、□□□□□□□□□□ という 8 個の空欄に、Y を 3 つ入れると残りは X となって道順が 1 つ定まることになります。つまり空欄を 3 つ取り出す組合せの総数が道順の総数に一致するので、求める個数は
 \[_8\mathrm{C}_3=56\]
と計算できます。

しかし、この道順問題はもっと簡単に、パズル的に解く方法が知られています。
 

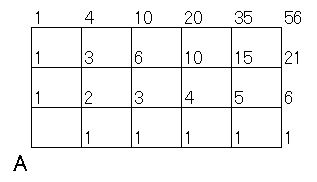
上の図のように各マスの隅に、そこまでに至る道順の数を書き込んでいけば、簡単に目的地に達する道順の総数を求めることができます。複雑な問題では、組合せ公式を使うと面倒な場合分けが必要ですが、この「書き込み方式」を使えば、ほとんどの問題を簡単に解決することができます。いくつかの例題で練習してみましょう。
 

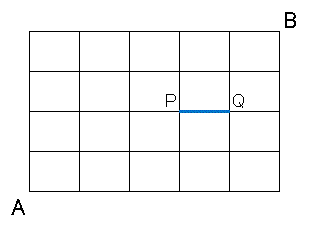
今度は PQ (青い線) を必ず通らなくてはならない、という条件をつけてみます。この場合は A から P までの道順の数と、Q から B までの道順の数をかければ答えが得られますね。
 \[_5\mathrm{C}_{2}\times\:_{3}\mathrm{C}_1=10\times 3=30\]
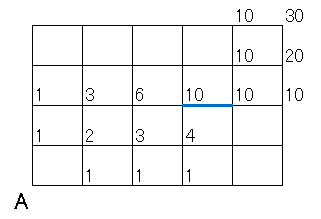
書き込み方式で解くと下の図のようになります。
 

 
次は下の図のような形をした市街地です。
 

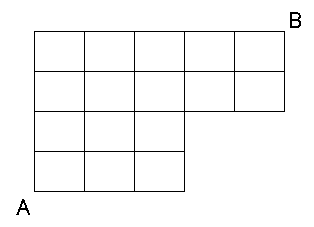
こういう変な形になると、組合せ公式では面倒ですので、迷わずに「書き込み方式」を選択しましょう。
 

 
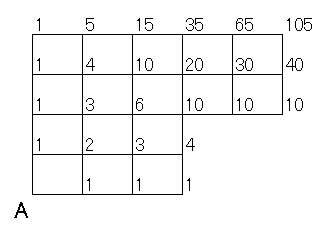
答えは 105 通りとなります。