【算数問題71】列車が追いつき、追い越します
長さ 120 m の列車 A が長さ 100 m の列車 B に追いついてから追い越すまで 44 秒かかります。また、長さ 80 m の列車 C が列車 B に追いついてから追い越すまで 12 秒かかります。列車 A と列車 C の速度の比が 5:6 であるとき、列車 A, B, C の速度はそれぞれ時速何 km ですか?
【ヒント】通過算 の問題です。列車 B に対する「相対速度」で考えてみましょう。
【解答71】下の図は列車 B に対し、列車 A と B が追いついたときの状態です(右から左へ走っていると考えてください)。
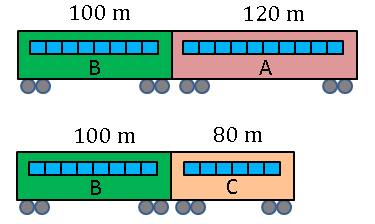
列車 A が列車 B を追い抜くということは、右端が 220 m 移動するということです。問題文にあるように、そのときにかかる時間は 44 秒です。つまり、列車 B からみた列車 A の速度(相対速度)は
220 m ÷ 44 秒= 5 m/秒
となります。同じようにして列車 B からみた列車 C の速度は
180 m ÷ 12 秒= 15 m/秒
です。それぞれの速度に列車 B の速度を加えれば、列車の外にいる人から見た速度が求められます。列車 A と列車 C の速度の比が 5:6 ですから、5 と 15 に同じ数を加えてこの比率 (つまり 50:60) になるようにすればいいので、列車 B の速度は 45 m/秒、列車 A と C の速度はそれぞれ 50 m/秒、60 m/秒です。km/時から m/秒への変換は
km/時 = 1000 m/3600秒
なので、m/秒から km/時への変換は 3.6 をかけます(この変換式は覚えておくと便利です!)。よって、A, B, C の速度はそれぞれ
180 km/時, 162 km/時, 216 km/時
となります。

エクセルや数学に関するコメントをお寄せください