確率密度と累積分布関数

確率密度

確率変数 $X$ が離散的で有限個の値
 $$x_1,x_2,\cdots ,x_n$$
をとるとき、$x_i(i=1,2,\cdots n)$ となる確率を
 $$P(X=x_i)=p_i$$
と表すことにします。これを全ての実数 $x$ に拡大した関数
 $$f(x)=\{\begin{array}{ll}{p}_i& (x=x_i)\\ 0& (x\ne x_i)\end{array}$$
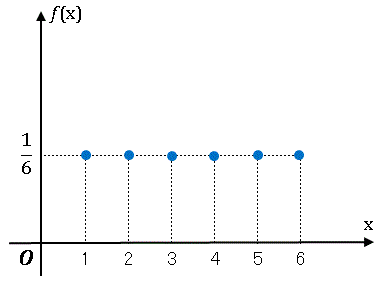
を 確率密度関数 (probability density function) あるいは単に 確率密度 (probability density) とよびます。本来なら値をもたない $P(X\ne x_i)$ を改めて「確率 0 」と定義した関数です。たとえばサイコロを 1 回投げて出た目を確率変数 $X$ とした場合、確率密度は
 $$f(x)=\{\begin{array}{ll}\frac{1}{6}& (x=1,2,3,4,5,6)\\ 0& (x\ne x_i)\end{array}$$
となります。つまり 6 個の点のみで 1/6 という値をもち、その他の全ての $x$ で 0 となるような関数です（下図参照）。
 

確率の和は 1 なので確率密度には
 $$\sum _{i=1}^{n}f(x_i)=f(x_1)+f(x_2)+\cdots +f(x_i)=1$$
という条件が付きます。

累積分布関数

確率変数が離散的な値をとる場合

確率変数 $X$ のとる値が $x$ 以下である確率を表すような関数
 $$F(x)=P(X\le x)=\sum _{x_i\le x}f(x)$$
を定義します。これを分布関数 (distribution function)、あるいは 累積分布関数 (cumulative distribution function) といいます。たとえばサイコロを 1 回投げて出た目を確率変数 $X$ とするとき、分布関数 $F(x)$ のグラフは次のように階段状になります。
 

 サイコロの出る目が 3 以下になる確率は
 $$F(3)=P(X\le x)=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=\frac{1}{2}$$
で与えられますが、$F(3.5)$ のように変数が整数以外の値をとった場合も、「出る目が 3.5 以下である確率」なので、これは「出る目が 3 以下である確率」に等しく、やはり $F(3.5)=1/2$ となります。また定義から明らかなように
 $$F(-\mathrm{\infty })=0,F(\mathrm{\infty })=1$$
が成り立ちます。確率変数が $\alpha <X\beta$ である確率は
 $$P(\alpha <X\le \beta )=F(\beta )-F(\alpha )=\sum _{\alpha <x_i\le \beta }f(x_i)$$
によって与えられます。

確率変数が連続的な値をとる場合

確率変数 $X$ が $a\le X\le b$ の範囲で連続的な値をとるときには、$X$ が $x$ と $x+\mathrm{\Delta }x$ の間にある確率が
 $$P(x\le X\le x+\mathrm{\Delta }x)={\int }_x^{x+\mathrm{\Delta }x}f(t)dt$$
となるような関数を確率密度 $f(x)$ と定義します。すべての確率の和は 1 となるので、$f(x)$ は
 $${\int }_a^{b}f(x)dx={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(x)dx=1$$
を満たしています。$X$ の値がある $x$ 以下である確率は
 $$P(X\le x)=F(x)={\int }_a^{x}f(t)dt={\int }_{-\mathrm{\infty }}^{x}f(t)dt$$
で求めることができます。また $X$ が $\alpha <X\le \beta$ の範囲の値をとる確率は
 $$P(\alpha \le X\le \beta )=F(\beta )-F(\alpha )={\int }_{\alpha }^{\beta }f(x)dx$$
となります。

ルーレット

下図のようなルーレット盤があるとします。
 

 
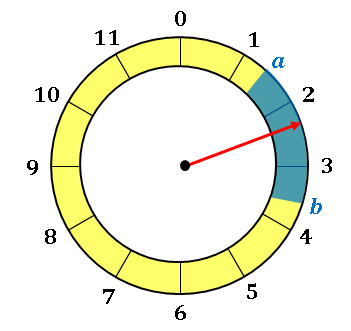
$a$ と $b$ は 0 から測った弧の長さです。
針が $a$ と $b$ の間に入る確率は $b-a$ に比例して
　
$$P(a\le X\le b)=k(b-a)$$
という形になっているはずです（$k$ は定数）。針がルーレット盤のどこかにある確率は 1 なので
　
$$P(0\le X\le 12)=12k=1$$
から $k=1/12$ が定まります。したがって
　
$$P(a\le X\le b)=\frac{1}{12}(b-a)={\int }_a^b\frac{dx}{12}$$
と書けるので、確率密度は
　
$$f(x)=\frac{1}{12}(0\le x\le 12)$$
であり、分布関数は
　
$$f(x)=\frac{x}{12}(0\le x\le 12)$$
で与えられます。