不等号の定義と不等式の性質

不等号の定義と不等式の解き方

この記事では数学における不等号の扱い方と不等式の解き方を解説します。

不等号

数学では実数の大小（順序）を表すために不等号（sign of inequality）とよばれる記号を用います。
 
・$a>b$  $a$ は $b$ より大きい ($a$ 大なり $b$)
・$a\ge b$  $a$ は $b$ 以上 ($a$ 大なりイコール $b$)
・$a<b$  $a$ は $b$ より小さい ($a$ 小なり $b$)
・$a\le b$  $a$ は $b$ 以下 ($a$ 小なりイコール $b$)
 
英語では、それぞれ次のように読まれています。
 
・$a>b$  $a$ is greater than $b$
・$a\ge b$  $a$ is greater than or equal to $b$
・$a<b$  $a$ is less than $b$
・$a\le b$  $a$ is less than or equal to $b$
 
ここに $a,b$ は実数の範囲内に限定されます。複素数同士の大小関係は定義されていません（ただし、複素数の絶対値であれば大小を比較できます）。

不等式の性質

不等号を含む式のことを不等式 （inequality）とよびます。特に不等式に未知数を含むとき、その未知数の範囲を求めることを「不等式を解く」といいます。不等式についての主な性質を並べておきます。

とくに $a=b$ のときは、$a=b=0$ の場合も含めて
 $$a^2\ge 0$$
という不等式が必ず成り立ちます（平方数は必ず正です）。

「$a$ が $1$ 以下であり、かつ $1$ 以上ならば $a$ は $1$ である」というような自明なことを述べているだけですが、様々な定理の証明で威力を発揮する重要な性質です。

たとえば $a$ が $3$ より小さな値だとします。$3$ は $10$ よりも小さいので、$a$ は $10$ よりも小さいといえます。

不等号の向きが同じ不等式が 2 つあれば、互いの左辺同士、右辺同士を加えた不等式も成立するということです。たとえば
 $$\begin{array}{rl}& 2<3\\ & 10<11\end{array}$$
という 2 つの不等式の両辺を加えて
 $$12<14$$
という不等式もまた成立しています。また、とくに $c=d$ のときは

が成り立ちます。すなわち、不等式の両辺に同じ数を加えても、その不等式はそのまま成り立ちます。

不等式の両辺に正の値をかけても不等号の向きは変わらず、負の値をかけると不等号の向きが反転します。とくに $c=-1$ とおけば

となります。たとえば $3<5$ という不等式において、両辺の符号を変える場合は不等号の向きが変わって $-3>-5$ という大小関係になります。

一次不等式

一次不等式は両辺に加減乗除の操作を加えるだけで簡単に解くことができます。たとえば
 $$\begin{array}{}\text{(1)}& x+5\ge 10\end{array}$$
という不等式を満たすような未知数 $x$ の範囲を求めてみます。不等式の両辺から同じ値を足しても不等号の向きは変わらないので（性質[5]）、両辺から $5$ を引いてみると（$-5$ を加えると）
 $$x\ge 5$$
というように $x$ の範囲が求められます。次はもう少し難しい問題です。
 $$\begin{array}{}\text{(2)}& 7x+3<31\end{array}$$
まずは両辺から $3$ を引いておきます。
 $$7x<28$$
次に「不等式の両辺に正の数をかけても不等号の向きは変わらない」という性質[5]を使います。両辺を $7$ で割って（$1/7$ をかけて）、
 $$x<4$$
となります。次は負の項を含む一次不等式を解いてみましょう。
 $$\begin{array}{}\text{(3)}& -3x>6\end{array}$$
両辺を $3$ で割ると
 $$-x>2$$
となります。この次の操作は慎重に行います。「両辺に負の値をかけると不等号の向きが変わる」という性質に注意して、両辺に $-1$ をかけると
 $$x<2$$
という解が得られます。少し難しい不等式の例題を解いてみましょう。

【解答】$c$ が正の値であるとき、$|x|<c$ を満たす $x$ は下の図の青い部分となります。
 

 
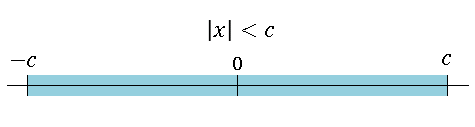
すなわち
 $$-c<x<c$$
です。したがって、不等式 $|x+2|<5$ において、$x+2$ のとりうる範囲は
 $$-5<x+2<5$$
となります。各辺から $2$ を引くと
 $$-7<x+2<3$$
という解が得られます。

【解答】$x\ge 0$ の範囲で $y=ax+b$ のグラフが正となるのは、下の A 図のような場合です。B 図のような場合は負になるところがあるので適しません。
 

 
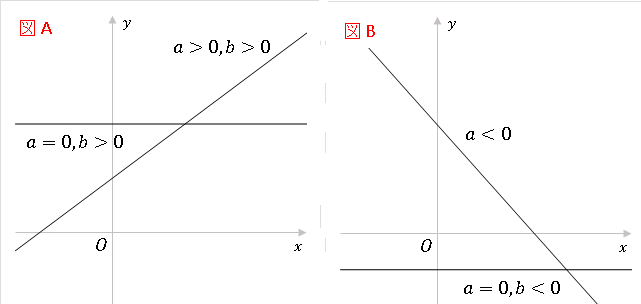
したがって、$a\ge 0,b>0$ が条件となります。