Excel VBA で作成した約数表と最大公約数表を掲載します。
約数表
自然数 1 ~ 100 の約数表です。
約数が 2 つしかない自然数は素数です。
| 自然数 | 約数 |
|---|---|
| 1 | 1 |
| 2 | 1, 2 |
| 3 | 1, 3 |
| 4 | 1, 2, 4 |
| 5 | 1, 5 |
| 6 | 1, 2, 3, 6 |
| 7 | 1, 7 |
| 8 | 1, 2, 4, 8 |
| 9 | 1, 3, 9 |
| 10 | 1, 2, 5, 10 |
| 11 | 1, 11 |
| 12 | 1, 2, 3, 4, 6, 12 |
| 13 | 1, 13 |
| 14 | 1, 2, 7, 14 |
| 15 | 1, 3, 5, 15 |
| 16 | 1, 2, 4, 8, 16 |
| 17 | 1, 17 |
| 18 | 1, 2, 3, 6, 9, 18 |
| 19 | 1, 19 |
| 20 | 1, 2, 4, 5, 10, 20 |
| 21 | 1, 3, 7, 21 |
| 22 | 1, 2, 11, 22 |
| 23 | 1, 23 |
| 24 | 1, 2, 3, 4, 6, 8, 12, 24 |
| 25 | 1, 5, 25 |
| 26 | 1, 2, 13, 26 |
| 27 | 1, 3, 9, 27 |
| 28 | 1, 2, 4, 7, 14, 28 |
| 29 | 1, 29 |
| 30 | 1, 2, 3, 5, 6, 10, 15, 30 |
| 31 | 1, 31 |
| 32 | 1, 2, 4, 8, 16, 32 |
| 33 | 1, 3, 11, 33 |
| 34 | 1, 2, 17, 34 |
| 35 | 1, 5, 7, 35 |
| 36 | 1, 2, 3, 4, 6, 9, 12, 18, 36 |
| 37 | 1, 37 |
| 38 | 1, 2, 19, 38 |
| 39 | 1, 3, 13, 39 |
| 40 | 1, 2, 4, 5, 8, 10, 20, 40 |
| 41 | 1, 41 |
| 42 | 1, 2, 3, 6, 7, 14, 21, 42 |
| 43 | 1, 43 |
| 44 | 1, 2, 4, 11, 22, 44 |
| 45 | 1, 3, 5, 9, 15, 45 |
| 46 | 1, 2, 23, 46 |
| 47 | 1, 47 |
| 48 | 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 |
| 49 | 1, 7, 49 |
| 50 | 1, 2, 5, 10, 25, 50 |
| 51 | 1, 3, 17, 51 |
| 52 | 1, 2, 4, 13, 26, 52 |
| 53 | 1, 53 |
| 54 | 1, 2, 3, 6, 9, 18, 27, 54 |
| 55 | 1, 5, 11, 55 |
| 56 | 1, 2, 4, 7, 8, 14, 28, 56 |
| 57 | 1, 3, 19, 57 |
| 58 | 1, 2, 29, 58 |
| 59 | 1, 59 |
| 60 | 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 |
| 61 | 1, 61 |
| 62 | 1, 2, 31, 62 |
| 63 | 1, 3, 7, 9, 21, 63 |
| 64 | 1, 2, 4, 8, 16, 32, 64 |
| 65 | 1, 5, 13, 65 |
| 66 | 1, 2, 3, 6, 11, 22, 33, 66 |
| 67 | 1, 67 |
| 68 | 1, 2, 4, 17, 34, 68 |
| 69 | 1, 3, 23, 69 |
| 70 | 1, 2, 5, 7, 10, 14, 35, 70 |
| 71 | 1, 71 |
| 72 | 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72 |
| 73 | 1, 73 |
| 74 | 1, 2, 37, 74 |
| 75 | 1, 3, 5, 15, 25, 75 |
| 76 | 1, 2, 4, 19, 38, 76 |
| 77 | 1, 7, 11, 77 |
| 78 | 1, 2, 3, 6, 13, 26, 39, 78 |
| 79 | 1, 79 |
| 80 | 1, 2, 4, 5, 8, 10, 16, 20, 40, 80 |
| 81 | 1, 3, 9, 27, 81 |
| 82 | 1, 2, 41, 82 |
| 83 | 1, 83 |
| 84 | 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84 |
| 85 | 1, 5, 17, 85 |
| 86 | 1, 2, 43, 86 |
| 87 | 1, 3, 29, 87 |
| 88 | 1, 2, 4, 8, 11, 22, 44, 88 |
| 89 | 1, 89 |
| 90 | 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90 |
| 91 | 1, 7, 13, 91 |
| 92 | 1, 2, 4, 23, 46, 92 |
| 93 | 1, 3, 31, 93 |
| 94 | 1, 2, 47, 94 |
| 95 | 1, 5, 19, 95 |
| 96 | 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96 |
| 97 | 1, 97 |
| 98 | 1, 2, 7, 14, 49, 98 |
| 99 | 1, 3, 9, 11, 33, 99 |
| 100 | 1, 2, 4, 5, 10, 20, 25, 50, 100 |
以下の配布用 Excel ブック (xlsx.ファイル) の divisor_table シートには、1 から 1000 までの約数表が掲載されています。
≫ divisor ブックをダウンロードする
約数表は VBA で次のようなコードを実行して作成しました。使ってみたい人はコピーして標準モジュールに貼り付けてください。
'[VBA] ある数 n のすべての約数を指定したセルに表示するプロシージャ Sub Divisor(n As Long, y As Long, x As Long) Dim k As Long, ct As Long '指定したセル番地(y, x)にnを書き込む Cells(y, x) = n 'あらゆる数は必ず1を約数にもつ Cells(y, x + 1) = 1 'カウンター変数の初期値 ct = 1 For k = 2 To n 'もしnがkで割り切れるならば If n Mod k = 0 Then 'カウンター変数を1増やす ct = ct + 1 'kを約数に追加する Cells(y, x + ct) = k End If Next k End Sub '[VBA] 約数表を作成するマクロ Sub Divisor_Table(p As Long, q As Long, y As Long, x As Long) Dim k As Long, j As Long j = 1 For k = p To q 'Divisorを呼び出す Call Divisor(k, y + j - 1, x) j = j + 1 Next k End Sub
約数表を作成する Divisor_Table には、サブルーチン Divisor が組込まれています。Divisor は任意の自然数 n とセル番地 (y, x) を指定して、n と n の約数を列挙させるプログラムです。アクティブシートのセル番地 (y, x) には n が表示され、その右隣のセルから小さい順にすべての約数が並びます。次のテストコードを実行してみてください。
'[VBA] Divisorのテストコード
Sub Test_Divisor()
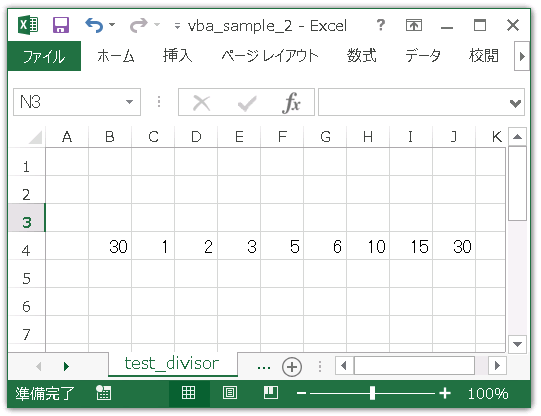
'30と30の約数をセル番地(4,2)に書き込む
Call Divisor(30, 4, 2)
End Sub
Test_Divisorを実行すると、下図のように約数が列挙されるはずです。
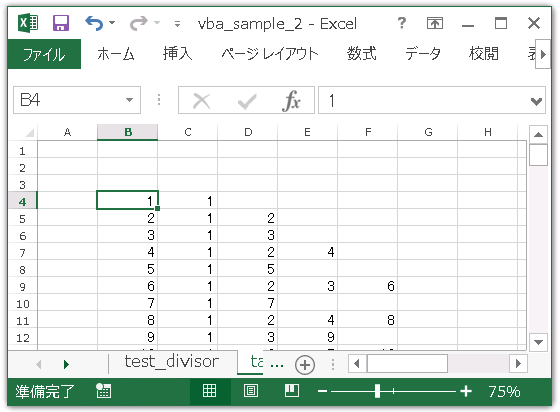
Divisor_Table の内部では、n と y を動かしながら Divisor を呼び出して約数表を作成します。次のコードはセル番地 (4, 2) を基点に 1 から 100 までの約数表を作成します。
'[VBA] Divisor_Talbeを使って約数表を作成する Sub Run_Divisor_Table() Call Divisor_Table(1, 100, 4, 2) End Sub
配布ファイルには、Divisor_Table によって作成した、1 から 1000 までの約数表が治められています。
VBAで公約数を求める
任意の自然数 a, b の公約数を計算して、ワークシートに書き出すコードも掲載しておきます。「a と b の最大公約数の約数は a, b の公約数である」であるという定理を用います。サブルーチン Divisor を再利用できるので、コードはシンプルです。
'[VBA] 自然数a,bのすべての公約数を指定したセルに表示するプロシージャ
Sub Common_Divisor(a As Long, b As Long, y As Long, x As Long)
Dim gcd As Long
'ワークシート関数gcdを呼び出す
gcd = WorksheetFunction.gcd(a, b)
'サブルーチンDivisorを呼び出す
Call Divisor(gcd, y, x)
'左端のセルを(a,b)に置き換える
Cells(y, x) = "(" & a & ", " & b & ")"
End Sub
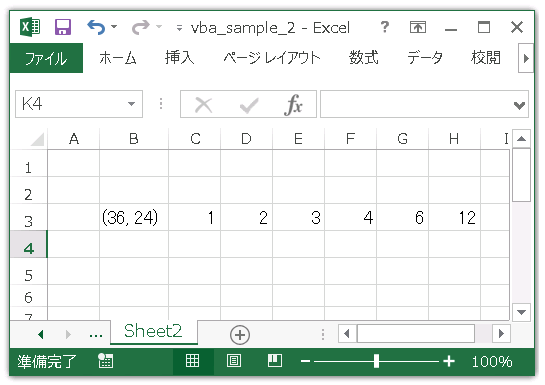
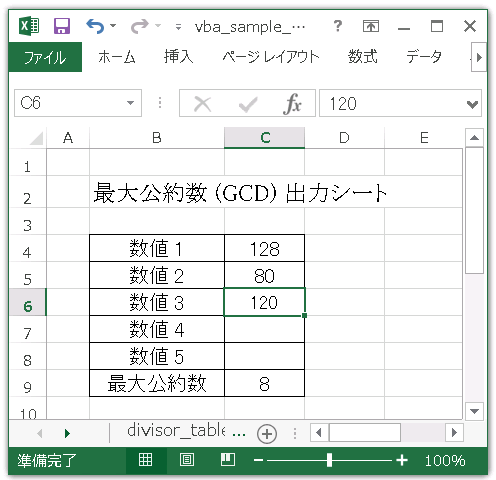
Common_Divisor で 36 と 24 の約数をすべて求めてみます。
'[VBA] Common_divisor のテストプロシージャ Sub Test_Common_divisor() Call Common_Divisor(36, 24, 3, 2) End Sub
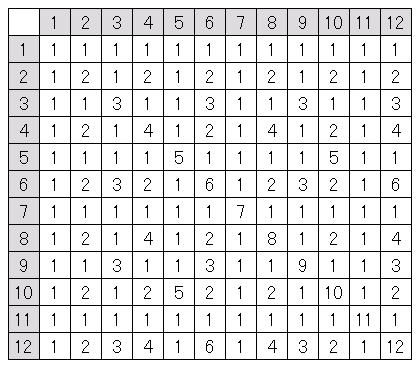
最大公約数表
(1, 1) ~ (16, 16) の 最大公約数表 も掲載しておきます。よければ画像をコピーしてお持ち帰りください。
Excel で最大公約数を求めるときには GCD 関数を使います。引数には 2 個以上の数値を渡せます。たとえば、セルに
=GCD(24, 18, 12)
と入力すると、24 と 18 と 12 の最大公約数 6 を返します。この関数を使って、上図のように任意の 2 数の最大公約数を調べるシートを作成できます。
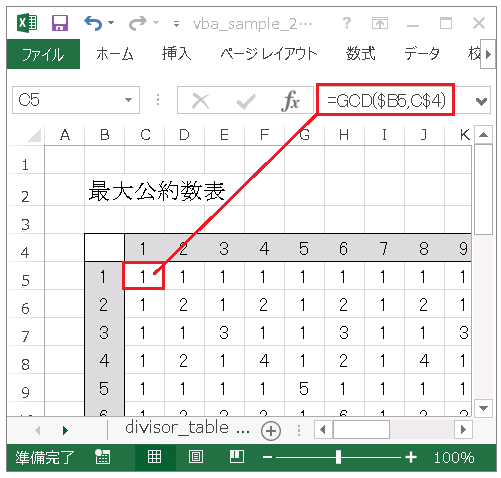
各セルで表の上端と左端の数値を参照できるように、複合参照スタイルで数式を入力しています。実際には、上の行と左の列を入力した後に、セル C2 に
=GCD($B5,C$4)
と入力して残りのセルにコピーしています。この最大公約数表は配布ファイルの gcd_table シートに掲載しています。配布ファイルの gcd シートには、最大 5 個までの数値の最大公約数を出力するシートを用意しています。
【補足】公約数と最大公約数
24 と 30 の約数を並べてみます。
24 の約数:1, 2, 3, 4, 6, 8, 12, 24
30 の約数:1, 2, 3, 5, 6, 10, 15, 30
24 と 30 の共通の約数、つまり公約数は
1, 2, 3, 6
であり、この中で最も大きな数 6 が最大公約数です。数論の記号を使って
(24, 30) = 6
と書くこともありますが、ベクトルや座標などと混同しやすいので注意が必要です。最大公約数は下図のように共通する約数で割れるところまで割って、左側の数を掛け合わせて得ることもできます。
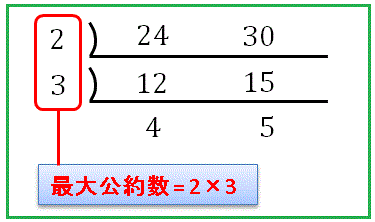
上の図から 24 と 30 を
24 = [2・3]・4, 30 = [2・3]・5
と書くことができます。[ ] の中が最大公約数です。そして残った 4 と 5 は互いに 1 以外の公約数をもっていません(もっていたら [] の中に入っているはずです)。なので、24 と 30 はともに係数 2・3 = 6 と、互いに 1 以外の公約数をもたない数 m, n を使って、
24 = 6 m, 30 = 6 n
というように書くことができます( m = 4, n = 5 )。ある未知の 2 数の最大公約数が与えられて、この「 m, n が互いに 1 以外の公約数をもたない」ということを「 m, n が互いに素である」という言い方をすることがあり、記号では
(m, n) = 1
と書きます。最大公約数は 1 であることを表しています。とくに整数問題では「互いに素である」ということはとても大切な概念ですので、これは絶対に覚えておいてください。慣れるために「互いに素である数」を上の記号を使って、いくつか載せておきます。
(1, 3) = 1, (4, 5) = 1, (3, 7) = 1, (5, 11) = 1, (13, 29) = 1
いずれのペアも互いに 1 以外の公約数をもっていないことを確認しておいてください。
【例題1】
(1) 48 と 72 の最大公約数を求めてください。
(2) 48 と 72 の最小公倍数を求めてください。
【解答】(1) 48 と 72 を共通の約数で割っていきます。
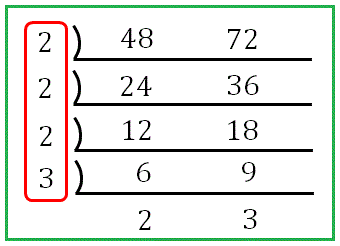
左側の数字を全部かけると
(48, 72) = 2・2・2・3 = 24
となります。
(2) 48 と 72 を素因数の積で表し、最大公約数を [] で括ると
48 = [2・2・2・3]・2 72 = [2・2・2・3]・3
と書くことができます。すると 48 に 3 を、72 に 2 をかけると同じ数になることがわかります。よって最小公倍数の記号 {} で表すと、
{48, 72} = 24・2・3 = 144
となります。
一般にある数 a と b が互いの最大公約数を用いて
a = [最大公約数] × m, b = [最大公約数] × n
と表せるとき、最小公倍数は
{a, b} = [最大公約数] × m n
と表すことができます。方程式を解ける人は次の問題にもチャレンジしてみてください。
【例題2】ある 2 つの自然数の最大公約数は 3 であり、最小公倍数は 18 です。また、その和が 15 であることがわかっています。この 2 つの数を求めてください。
【解答】求める数を a, b (a < b)とおきます。 a と b の最大公約数が 3 ですから、互いに素な m, n を用いて
a = 3 m, b = 3 n
と書くことができます。足して 15 ですから、
3 m + 3 n = 15 ∴ m + n = 5
最小公倍数が 18 なので、
3 m n = 18 ∴ m n = 6
掛けて 6 となる自然数のペアは
1 と 6, 2 と 3
の 2 通りしかありませんが、このうち足して 5 になるのは 2 と 3 ですから、
a = 3・2 = 6, b = 3・3 = 9
となります。

エクセルや数学に関するコメントをお寄せください