平均算の解き方
平均算とは、読んで字のごとく平均を扱う問題です。平均とはいくつかの数量を均したもので、次のように定義されています。
平均 = 合計値 ÷ 個数
ストレートに平均を計算させる問題よりも、予め平均が与えられていて、そこから個数を問う問題のほうが多いようです。
【平均算の例題01】コンビニでお菓子を買います
最初に平均算の簡単な練習問題を解いてみましょう。
【例題】コンビニでお菓子を 4 つ買いました。値段は 220 円、270 円、290 円、380 円でした。平均の金額はいくらですか?
【解答①】まずはお菓子 4 個の値段を合計します。
220 + 270 + 290 + 380 = 1160 円
これを 4 で割ると平均は
1160 ÷ 4 = 790 円
となります。
【解答②】あまりに簡単な問題で驚かれたかもしれませんが、実はこの問題、平均の暗算練習用に用意したのです。4 つ足して 4 で割るという計算も暗算できないことはないですが、こういう場合は凸凹を均すという考え方で計算した方が簡単です。お菓子の値段はそれぞれ
220 円、270 円、290 円、380 円
となっています。ここで「ちょっと高すぎる」と思われる 380 円から 90 円を取り置いて次に高い値段に合わせ、取ったお金は別の場所に置いてみます。
220 円、270 円、290 円、290 円 (90 円)
() の中がいったん取り置かれた金額です。これを 220 円と 270 円が等しくなるように分配すると
290 円、290 円、290 円、290 円
と 4 つのお菓子の値段が揃って平均が 290 円であることがわかります。以上のような操作を頭の中で行う習慣が身につくと、平均算に対する数感覚が養われます。取り置き方などは色々あるので、問題の状況に応じて臨機応変に対処します。
【平均算の例題02】書店で本を買います
こばとちゃんは書店で 5 冊の本を買うと平均して 1000 円でした。また、5 冊のうち 1 冊は 1600 円でした。残り 4 冊の値段の平均はいくらですか?
【解答】合計 = 平均 × 個数によって 5 冊の合計金額を求めます。
1000 × 5 = 5000 円
1600 円を差し引くと、残り 4 冊の本の金額の合計は
5000 - 1600 = 3400 円
となります。これを 4 で割ると、残り 4 冊の平均は
3400 ÷ 4 = 850 円
となります。
【平均算の例題03】合格者の人数は?
ある試験が行われ、450 人が受験しました。受験者全体の平均点は 59 点で、合格者の平均点は 68 点、不合格者の平均点は 53 点でした。合格者の人数を求めてください。【公務員試験 H14市役所】
【解答①】図を描くと一瞬でわかる問題なのです。
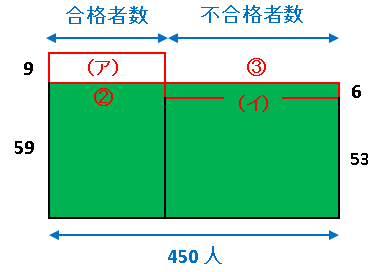
合格者の平均点は 68 点ですから平均の 59 点より 9 点高く、また不合格者数の平均点は 53 点なので平均点より 6 点低くなっています。図の赤枠で囲んだ長方形(ア)と(イ)が平均からのずれを表しています。平均からはみだしている(ア)の部分を取って(イ)の部分に埋めると、合格者数と不合格者数の合計点は緑色に塗られた長方形になるはずです。つまり(ア)と(イ)の面積は等しいはずなのです。ここで
(ア)と(イ)の縦の長さの比 = 9:6 = 3:2
となっているので、横の長さの比は逆に 2:3 となっているはずですね。なので合格者の数は
450 × 2/5 = 180 人
となります。こういう問題も慣れてくると、平均からのずれの 9 と 6 だけで暗算できます。
【解答②】方程式を使って解くこともできます。
合格者数を x とおくと、不合格者数は 450 – x です。
合格者の合計点数は 68x 、不合格者の合計点数は 53(450 - x) で、その合計が平均点 × 受験者数に等しいのですから、
68x + 53(450 - x) = 59 × 450
15x = 59 × 450 - 53 × 450
15x = 6 × 450
∴ x = 6 × 30 = 180 人
となります。

エクセルや数学に関するコメントをお寄せください