【損益算】仕入れ値（原価）・定価・利益の計算

損益算とは読んで字の如く「損するのかな？　それとも得をする（益を得る）のかな？という計算をする問題です。要するに物の売り買いを題材に仕入れ値（原価）、定価、利益、割引、消費税などを問われる類の問題です。中学入試や SPI に頻出する算数の代表選手ともいえる分野ですから、スマートな解法手順を身につけておきたいところです。　

売り値と仕入れ値・利益の関係

損益算を解くには「売り値と仕入れ値、利益の関係」を押さえておく必要があります。常識的なことではありますけど、念のために確認しておきましょう。

商品１個あたりの利益 = 売り値 - 仕入れ値  [1]

これが基本です。また、定価と売り値、割引額の間には

定価 = 売り値 + 割引額  [2]

という関係があります。式 [1] と [2] から

定価 = 仕入れ値 + 利益 + 割引額  [3]

という関係を得ることもできます。これらをまとめて棒グラフで表すと次のようになります。
 

 
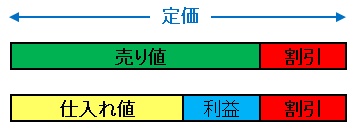
複雑な問題を解くときは、このような図を描いて状況を把握します。それでは基本的な問題で損益算を練習してみましょう。

【例題01：損失の回避】1 個 10 円の卵を 500 個仕入れて、1 個 13 円で売ります。損失が出ないようにするには最低何個売り捌く必要がありますか？
 
【解答】仕入れ額の合計は
 
  500 × 10 = 5000 円
 
です。これを売り値の 13 円で割ると
 
  5000 ÷ 13 = 384 ⋅⋅⋅ 8
 
となります。余りがあることに注意です。384 個では若干の損が出るということです。よって答えは 385 個となります。

次は定価と売り値、割引の関係を問う問題です。
 
【例題02：定価はいくら？】ある商品を定価の 2 割引の 1200 円で売っています。この商品の定価はいくらですか？
 
【解答1】定価と売り値、割引の関係を描くと下の図のようになります。
 

○で囲んだ数字は比率を表しています。つまり定価の 2 割に相当するのが割引額なので、売り値⑧に対して割引額が②という関係になってます。簡単にすると売り値④に対して割引額①です。ということは売り値④に対して定価は⑤です。ここで 1200 円というのは 300 円が 4 つと考えると、定価は 300 円が 5 つということになります。つまり
 
  定価 = 300 × 5 = 1500 円
 
となります。慣れてくると、
 
 定価の 2 割引きで 1200 円？
 それなら、売り値と定価の比率は 8：10 だね。
 だから、売り値は 300 × 5 = 1500 円だよ。
 
という具合に暗算で計算することができます。何か特別なセンスが必要というわけではなく、こういう解き方を繰り返して慣れるというだけのことです。

【解答2】方程式で解くこともできます。求める定価を x とすると、そこから 2 割を差し引いた金額が売り値なので
 
  (1 – 0.2)x = 1200
 
となります。これを解いて x = 1500 円が得られます。
　
次は損益算な中でもちょっと難しい部類の問題です。
 
【例題03：チョコレートの仕入れ値】1 個あたり同じ金額で仕入れたチョコレートがあります。このチョコレートを 1 個 300 円で 30 個売ったときの利益と 1 個 260 円で 40 個売ったときの利益は同じです。チョコレートの仕入れ値はいくらですか？
 
【解答1】次のような面積図を描いてみます。
 

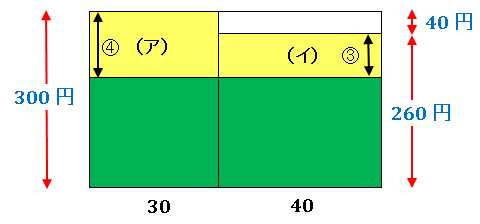
黄色い部分が利益を表す面積です。問題文では（ア）と（イ）が等しいと言っています。その底辺はそれぞれ 30 と 40 で、その比率は 3：4 です。ということは、互いの面積を等しくするためには縦の長さは逆に 4：3 の比率になっている必要があります（図で○で囲ってある数字が比率を表しています）。
 
すると、図にあるように①に相当するのが 40 円です。
よって、（ア）の縦の長さが 40 × ④ = 160 円となります。
仕入れ値は緑の長方形の縦の長さですから、
 
  300 – 160 = 140 円
 
が答えとなります。

【解答2】方程式で解く場合は仕入れ値を x とおいて、
 
  30(300 – x) = 40(260 – x)
 
という式が立てられます。これを解いて x = 140 円となります。
 
≫ 消費税を速算してみましょう！
≫ 中学入試レベルの「損益算」超難問に挑戦してみましょう！