【Excel】tanθのグラフを描く方法

新しいシートを用意してください。
今回は $y=\tan\theta$ のグラフに挑戦です！
　

エクセルでtanθのグラフをプロットします

$\sin\theta$ や $\cos\theta$ に比べて、$\tan\theta$ はとても厄介な関数です。その理由は無限大に発散する関数だからです。とりあえず、$-\pi/2\leq\theta\leq\pi/2$ に限定して考えると、
 \[\begin{align*}\\[6pt]
\theta\rightarrow-\pi/2\:：\:\tan\theta&\rightarrow-\infty\\[6pt]
\theta\rightarrow\pi/2\:：\:\tan\theta&\rightarrow+\infty\end{align*}\]
となりますね。数値計算では ∞ という概念を正確に再現することはできません（それは紙に描いたグラフでも同じですが）。そこで、この発散の様子を「いかにもそれらしく」描かせるというテクニックが必要になってきます。

区間の両端で急勾配をとる関数なので、$\theta$ の小さな変化に対して $\tan\theta$ の変化がとても大きいということです。あまり大刻みなデータを作るとグラフがギザギザになってしまいます。Excel には各点を滑らかにつなぐ「平滑線作成」機能が備わっていますが、あまりに大雑把なデータを入れると、やはりギザギザなグラフを出力します。そこで、$\theta$ の増分 $\Delta\theta$ をなるべく小さくすることによって、滑らかなグラフの再現を試みてみます。

最初に $\theta=-\pi/2$ に近い点のデータを作ります。
データがわかりやすいように、角度θを度数単位で並べて、tan 関数に渡すときにラジアン単位に変換するようにします。

=tan(radians(－90))

としてもエラーを返されるので -90 はデータから除外しておきます。セル A2 には「-89.9」というぎりぎりの値を入力しておきます。A3 には「-89.8」と入れておきます。そして値が -89 になるまでオートフィル。これで + 0.1° 刻みのデータが埋め込まれました。
 
-89° から +89° までは 1° 刻みでデータを作成します。前回までの 10° 刻みに比べるとデータの数が多いので、オートフィルではなく別の方法でデータ系列を作ります。「ホーム」タブをクリックして上部右端のほうにある “↓” マークのついた「フィル」を選択します。縦にメニューが表示されるので、「連続データの作成」を選びます。
 

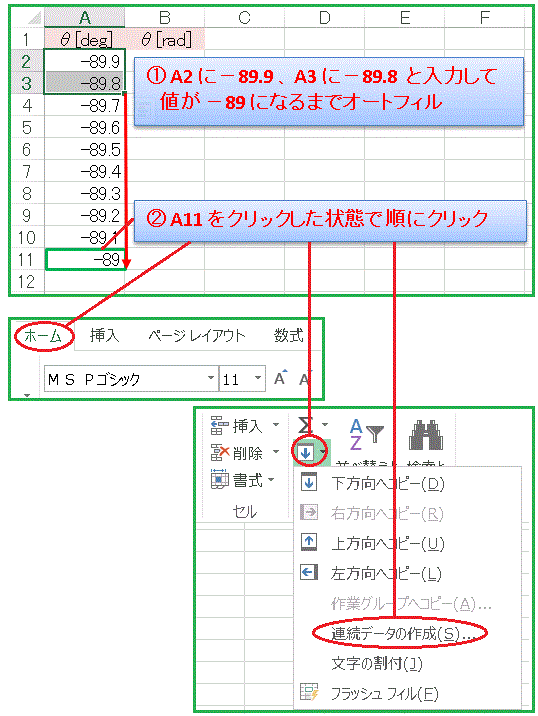
すると、次のような画面が現れるので、範囲の「列」にチェックを入れ、増分値に「1」、停止値に「89」と入力して、「OK」ボタンをクリックします。
 

 
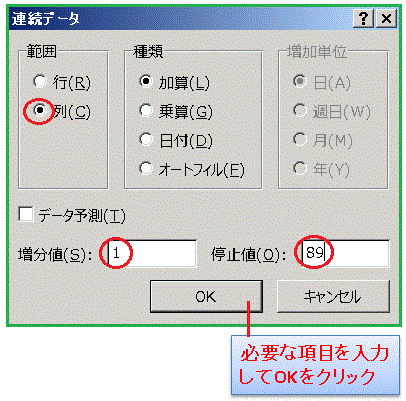
これで 1° 刻みで 89 までのデータが入ります。残りのデータを作りましょう。下のほうへ画面をスクロールして、セル A 190 に「89.1」と入力し、セル A189 と A190 を選択します。そしてやはり端のぎりぎりの値である 89.9 のところまでオートフィルです。
 

これで θ のデータは完成しました。
θ をラディアンに変換したデータを B2 に作ります。

=radians(a2)

と入力します。セル C2 には

=tan(b2)

と入力して tanθ を計算させます。セル B2 と C2 をまとめて選択して右下隅をダブルクリックしてデータを完成させます。そのあと A 列と C 列を同時選択して（ ctrl キーを押しながら A と C をクリック）、「挿入」⇒「散布図」⇒「平滑線」の順にクリックすれば、tanθ のグラフが出力されます。
 

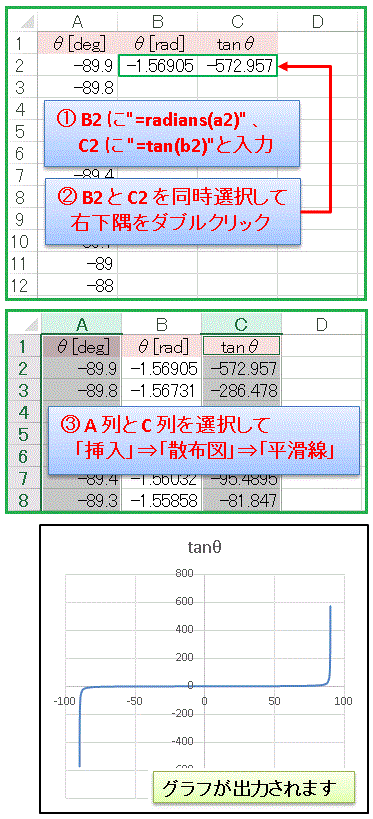
「 … 見慣れた tanθ のグラフと少し違うような」と思われるかもしれませんが、初期設定の最大値が大きすぎるので、下にべたっと張り付いたようなグラフになってしまっているのです。以前に学んだように軸の設定画面から、縦軸の最大値を「20」、最小値を「-20」に設定し、横軸の最大値を「90」、最小値を「-90」、目盛間隔を「30」に設定してください。ついでにお好みで色を変えたりタイトルをつけてみましょう。下図のようになるはずです。
 

 
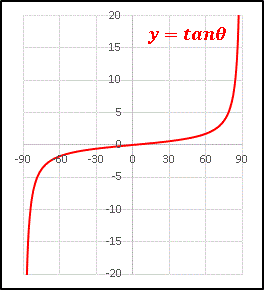
両端でも滑らかにつながるグラフになっていますね。今回学んだことは分数関数や対数関数のグラフを描くときにも応用できます。こうしたグラフの描き方も順次紹介していく予定なので、お楽しみに！