余弦定理の意味

【Excel】余弦定理の解析

三角比を学び始めると比較的早い段階で正弦定理と余弦定理を習うと思いますが、それだけ応用範囲が広く使い勝手の良い定理なのです。今回は余弦定理の意味を微積分を用いて探ってみたいと思います。
 

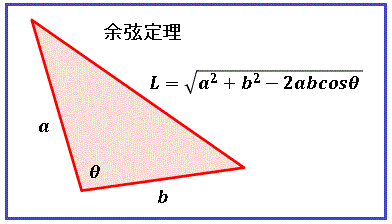
余弦定理は上図にあるように、三角形のある頂点の向かいにある辺の長さ L は頂点をはさむ辺の長さ a, b によって
 $$\begin{array}{}\text{(1)}& L(\theta )=\sqrt{a^2+b^2-2abcos\theta }\end{array}$$
と表せるというものです。いわば（直角三角形に用いる）ピタゴラスの定理（三平方の定理）の一般バージョンです。実際、$\theta =\pi$ でピタゴラスの定理と一致します。
 
$\theta <\pi /2$ ならば、$\cos \theta$ は正なので、√ の中身にある $a^2+b^2$ から値が少し引かれて、ピタゴラスの定理で得られる直角三角形の辺の長さよりも短くなります。
 
$\theta >\pi /2$ なら $\cos \theta$ は負となって、逆に直角三角形の辺の長さよりも長くなります。

辺の長さを固定して余弦定理を考えます

さて、ここでちょっとこんなことを考えてみます。下図のように二辺が $1$ の二等辺三角形を考えて、$\theta$ をどんどん大きくして三角形を広げていくのです。
 

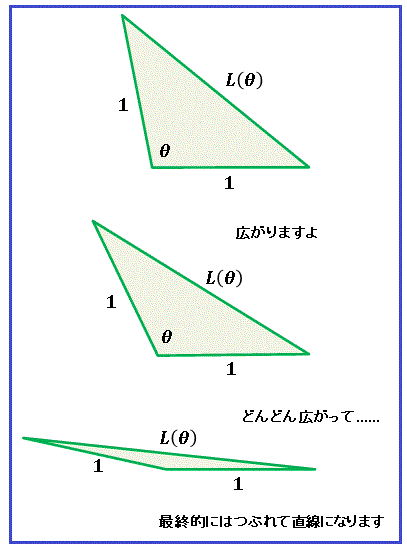
すると最後には三角形は潰れてしまって、$L(\theta )$ は二辺を足した長さ $2$ に等しくなるはずです。公式 (1) で $a=b=1$ とおくと
 $$\begin{array}{}\text{(2)}& L(\theta )=\sqrt{2(1-cos\theta )}\end{array}$$
$\theta =\pi$ を代入すれば $L(\theta )=2$ となりますね。
辺の長さが増加する様子を Excel のグラフで確認してみます。
 

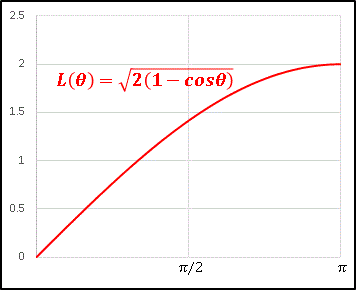
$\theta$ が $\pi$ に近づくほど増加率が落ちているのが気になるところです。$L(\theta )$ を微分して詳しく解析してみましょう。無理関数の微分は少し面倒なので、
 $$L^2=2(1-\cos \theta )$$
の形で両辺を $\theta$ で微分します：
 $$L\frac{dL}{d\theta }=\sin \theta$$
$L$ の表式を再度代入して
 $$\begin{array}{}\text{(3)}& \frac{dL}{d\theta }=\frac{sin\theta }{\sqrt{2(1-cos\theta )}}\end{array}$$
が得られます。Excel でグラフを描いてみると …
 

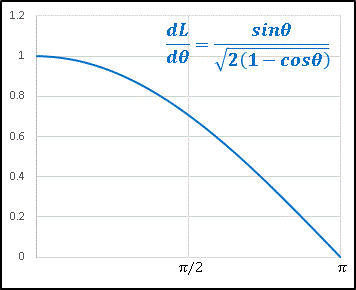
角度が非常に小さい時には、角度 +1[rad] に対して対辺の長さも +1 という割合で急増します。角度が開いていくにしたがって増加率は減少し、$\theta =\pi$ に近いところでは $\theta$ の変化にともなう対辺の増加はほとんどありません。

角度を固定して余弦定理を考えます

今度は $\theta =\pi /3$ に固定して、一辺の長さを下図のように直線に沿って変化させます。
 

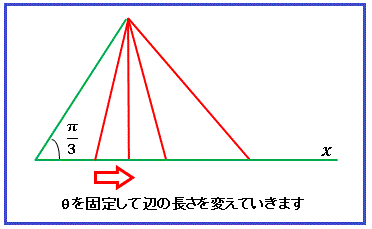
公式 (1) で $a=1,b=x,\theta =\pi /3$ とおくと
 $$\begin{array}{}\text{(4)}& L(x)=\sqrt{x^2-x-1}\end{array}$$
という式が得られます。グラフは次のようになります。
 

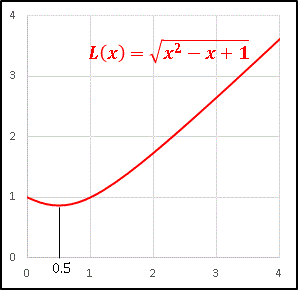
今度は辺の長さ $x$ によって三角形の形が決まります。
グラフではちょうど $x=1/2$ のところ、すなわち直角三角形になるところを境にして辺の長さは減少から増加に転じています。$x$ はいくらでも大きくできますから、この場合の $L$ は $x\to 1$ で発散します。無限大の長さの辺というのも想像しにくいですけどね … 。