接線を引いてみましょう

　この記事では、エクセル で作成したグラフの任意の点に 接線 を引く方法を解説します。

エクセルで曲線上に接線を引いてみます

　放物線 $f(x) = x^2 + x$ の指定した点に接線を引いてみます。
　関数 $y = f(x)$ の点 $a$ における微分係数を $f'(a)$ とすると、接線の方程式は
　
\[y = f'(a)(x – a) + f(a)\]
で求めることができます。$f'(a)$ については
　
\[f'(a)=\lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h}\]
で計算することができます。$f(x) = x^2 + x$ の場合は
　
\[f'(a)=\lim_{h\rightarrow 0}\frac{(a+h)^2+a+h-(a^2+a)}{h}=\lim_{h\rightarrow 0}\frac{(a+h)^2+h-a^2}{h}\]
という式を用いることになります。
　
　まずは接線のデータを用意します。セル F2, F3, F4, F5 には、それそれ「 h 」、「 a 」、「 fa 」、「 m 」という 名前を定義しておきます 。

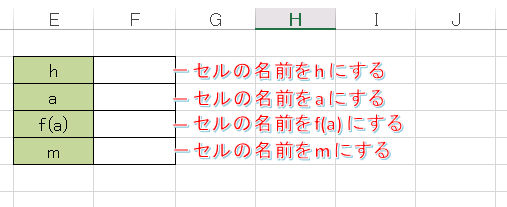
　セル F2 には h の値を入力します。

=1E-8

　セル F3 には接線を引きたい点を指定します。とりあえずは

=1

と入力しておきましょう。セル F4 には上で指定した a に対応する関数の値 f(a) を入力します。

=a^2+a

　セル F5 には接線の傾き m = f'(a) を入力します。

=((a+h)^2+h-a^2)/h

　
　次は二次関数 $f(x) = x^2 + x$ のデータを作りましょう。

　

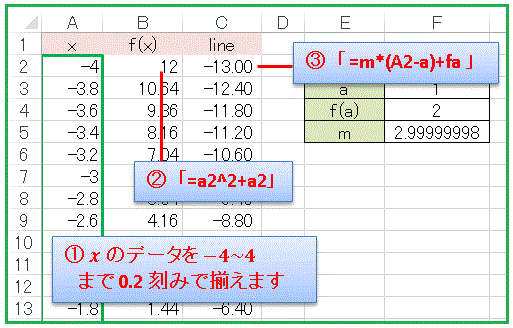
　A 列に x の値を －4 ～ 4 まで作成します。セル B2 には各点に対応する関数値

=a2^2+a2

と入れて、セルの右下隅をダブルクリックしてデータを揃えます。そして C 列には接線の方程式を作ります。先ほど入力した m, a, fa を名前で参照して、セル C2 に

=m+(A2-a)+fa

と入れて右下隅をダブルクリックです。これで全てのデータが揃いました。 A 列と B 列を選択して二次関数のグラフを作成してから、C 列のデータを追加し、適度に軸の範囲を調整すると、次のようなグラフになるはずです。

　

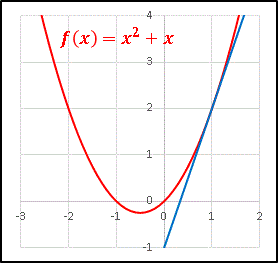
　a の値を変えると接線も変化します。a = -2 としてみると …

　

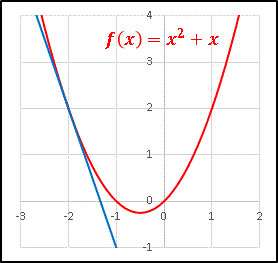
　ちゃんと x = -2 の所に接線が引かれていますね！