【Excel】exp(1/x)の解析
e の x 乗根 というシンプルな関数です。しかし、いざグラフを描こうとしても「不連続点」という厄介な問題が立ち塞がります。式の形から単調減少であることはすぐ分かると思いますが、一応微分して確かめてみます。この手の関数の微分は両辺の対数をとると簡単に計算できます。すなわち
\[\log y=\frac{1}{x}\]
の形にしてから両辺を $x$ で微分すると
\[\begin{align*}\frac{d(\log f)}{dx}\frac{df}{dx}&=-\frac{1}{x^{2}}\\\frac{1}{f}\frac{df}{dx}&=-\frac{1}{x^{2}}\\\frac{df}{dx}&=-\frac{e^{1/x}}{x^{2}}\end{align*}\]
$f'(x)$ は常に負で、$f(x)$ は単調減少関数です。$f'(x)$ をもう1度微分して
\[f^{\prime\prime}(x)=\frac{(1+2x)e^{1/x}}{x^{4}}\]
を得るので、$f(x)=0$ とおいて変曲点
\[(x,\:y)=\left(-\frac{1}{2},\:\frac{1}{e^2}\right)\]
が存在することが分かります。さらに $f(1)=e$ であり、また $x\rightarrow\pm\infty$ での極限は
\[\lim_{x\rightarrow\pm\infty}f(x)=1\]
となり、$y=1$ が漸近線となっています。さて、ここからが問題となるところですが、 $x\rightarrow 0$ の極限はどうなるでしょう。実はこの点に関しては慎重な扱いが必要です。 $x\rightarrow +0$(正の側から $\theta$ に近づく極限)と $x\rightarrow -0$ (負の側から $0$ に近づく極限)の値が異なっているからです:
\[\begin{align*}\lim_{x\rightarrow +0}f(x)&=\lim_{x\rightarrow +0}e^{1/x}=\infty\\\lim_{x\rightarrow -0}f(x)&=\lim_{x\rightarrow 0}e^{-1/\left| x\right|}=\lim_{x\rightarrow 0}1/e^{1/\left| x\right|}=0\end{align*}\]
つまり原点はこの関数の不連続点となっています。以上の情報をもとにグラフを描くと …
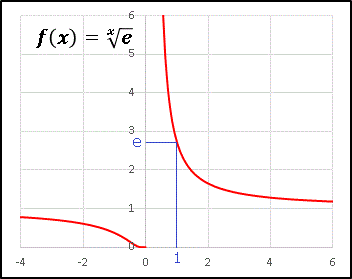
$x=0$ を境に関数の値が「飛んで」しまっています。このような簡単な表式の関数で不連続点が現れてしまうことは、ちょっと驚きですね。次はもう少し複雑な不連続関数を見てみましょう。先程扱った $e^{1/x}$ が分母に含まれていますから、微分しなくても、この関数が単調増加であることがわかります。やはり $x=0$ が不連続点となります。先ほど計算した $e^{1/x}$ の極限値を使えば、
\[\begin{align*}\lim_{x\rightarrow +0}f(x)&=0\\\lim_{x\rightarrow -0}f(x)&=1\end{align*}\]
となることがすぐにわかります。グラフを描いてみましょう:
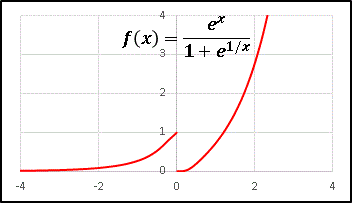
今度は不連続点を境に有限の極限値をとっています。

エクセルや数学に関するコメントをお寄せください