ベルヌーイらせん（等角螺旋）

ベルヌーイらせん(Bernoulli Spiral)

次のような微分方程式を考えます。
 $$\begin{array}{}\text{(A)}& \frac{dy}{dx}=\frac{x+y}{x-y}\end{array}$$
これは同次型なので、$y=ux$ とおくと $y^{\prime }=u+x{u}^{\prime }$ なので
 $$u+x\frac{du}{dx}=\frac{1+u}{1-u}$$
となります。変数分離すると
 $$\frac{1-u}{1+u^2}du=\frac{dx}{x}$$
すなわち
 $$(\frac{1}{1+u^2}-\frac{u}{1+u^2})du=\frac{dx}{x}$$
両辺を積分すると
 $$\mathrm{Arctan}u-\frac{1}{2}\log (1+u^2)=\log |x|+c$$
変数を $y$ に戻して式を整理すると
 $$\begin{array}{}\text{(A1)}& \mathrm{Arctan}\left(\frac{y}{x}\right)-\frac{1}{2}\log (x^2+y^2)=c\end{array}$$
となります。ここで $x=r\cos \theta ,y=r\sin \theta$ によって変数を極座標に変換すると、
 $$\frac{y}{x}=\tan \theta ,x^2+y^2=r^2$$
となるので、これを (A1) に代入して
 $$\log r=\theta -c$$
$A=e^{-c}$ とおくと
 $$r=A{e}^{\theta }$$
という極座標表示の解が得られます。この形から明らかなように、動点は $\theta$ の増加とともに原点から遠ざかるので、解曲線はらせん状にになります。
 

 
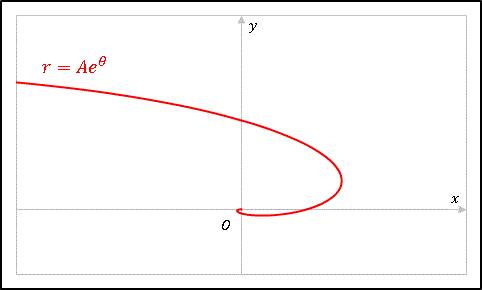
スイスの数学者ベルヌーイ (Bernoulli) によって発見されたことから、この曲線はベルヌーイらせん（ベルヌイ螺旋）とよばれます。あるいはその形状から単に対数らせんまたは等角らせんとよばれることもあります。

同次型微分方程式の解の極座標表示

ベルヌーイらせんの例で見たように、同次型方程式の解を極座標で表すことを考えてみます。結論から言うと、

これを証明してみましょう。$x$ は $r$ と $\theta$ の 2 変数関数なので、その微増分は全微分によって、
 $$\begin{array}{rl}dx& =\frac{\partial (r\cos \theta )}{\partial r}dr+\frac{\partial (r\cos \theta )}{\partial \theta }d\theta \\ & =dr\cos \theta -r\sin \theta d\theta \end{array}$$
のように表されます。$dy$ についても同様にして
 $$dy=dr\sin \theta +r\cos \theta d\theta$$
と表せます。したがって
 $$\frac{dy}{dx}=\frac{dr\sin \theta +r\cos \theta d\theta }{dr\cos \theta -r\sin \theta d\theta }=\frac{r^{\prime }\tan \theta +r}{r^{\prime }-r\tan \theta }$$
となります。ただし $r^{\prime }=dr/d\theta$ とおきました。これを
 $$\frac{dy}{dx}=f(y/x)=f(\tan \theta )$$
に代入して整理すると
 $$\frac{dr}{d\theta }=\frac{f(\tan \theta )\tan \theta +1}{f(\tan \theta )-\tan \theta }r$$
となります。
 $$F(\theta )=\frac{f(\tan \theta )\tan \theta +1}{f(\tan \theta )-\tan \theta }$$
とおくと、
 $$\frac{dr}{d\theta }=rF(\theta )$$
変数分離して解くと
 $$r=A\exp [\int F(\theta )d\theta ]$$
という解が得られます。ベルヌーイらせんを解にもつ微分方程式
 $$\begin{array}{}\text{(A)}& \frac{dy}{dx}=\frac{x+y}{x-y}\end{array}$$
に上の公式を適用してみます。
 $$f(u)=\frac{1+u}{1-u}$$
なので、
 $$f(\theta )=\frac{1+\tan \theta }{1-\tan \theta }$$
これを $F(\theta )$ の表式に代入すると
 $$F(\theta )=\frac{1+{\tan }^2\theta }{1-{\tan }^2\theta }=1$$
となります。したがって
 $$r=A\exp [\int d\theta ]=A{e}^{\theta }$$
という解が得られます。