乗算表（乗法表）を用いて一次合同方程式を解く

乗算表（乗法表）

ある法 (mod) における剰余類ごとの掛け算をまとめた乗算表（乗法表）を用意しておくと計算するときに便利です。特に合同式の割り算をするときには重宝します。$\mathrm{mod}\;7$ における乗算表は次のようになります。



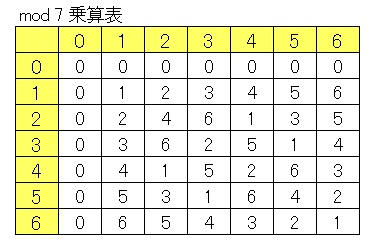
たとえば $x\equiv 4\times 5\:(\mathrm{mod}\;7)$ を求めたいときは、対応する数字が交差するところを見ます。$6$ という数字があるので、$x\equiv 6\:(\mathrm{mod}\;7)$ であることがわかります。もちろん合同式なので実際には
\[C_4\times C_5=C_6\:(\mathrm{mod}\;7)\]
という計算をしているわけで、$C_6$ に属する
\[x\equiv \cdots\:-8,\:-1,\:6,\:13,\:20,\:\cdots\:(\mathrm{mod}\;7)\]
のどれもが答えとなります。普通は一番小さな正数を代表に選んで答えますが、合同式の計算は剰余類同士の演算であることは常に頭に入れておく必要があります。

一次合同方程式

$x\equiv 4\times 5\:(\mathrm{mod}\;7)$ のような掛け算の場合は、わざわざ表など使わなくても $4\times 5=20$ を $7$ で割れば $6$ 余ることはすぐにわかるので、乗算表の有難味はほとんどありません。乗算表は主に割り算で用います。たとえば合同式で $5\div 3$ という割り算をすることは、
\[3x\equiv 5\:(\mathrm{mod}\;7)\]
を満たすような $x$ を求めるということです。このような方程式を一次合同方程式（linear congruence equation）とよびます。上の方程式を乗算表を使って解いてみます。まず黄色く塗られた部分の $3$ という数字のある行（または列）から $5$ という数字を見つけます。対応する列（または行）が $4$ なので、解は $x\equiv 4\:(\mathrm{mod}\;7)$ であることがわかります。



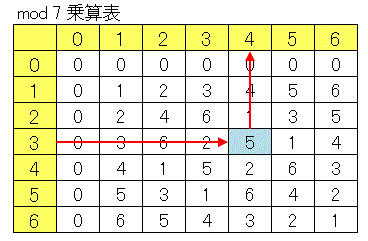
つまり合同式では
\[5\div 3\equiv 4\:(\mathrm{mod}\;7)\]
という計算式が成り立つのです。このあたりの感覚は最初のうちは戸惑いますが、訓練を重ねるうちに慣れてきます。しかし $6\div 2$ のような計算、すなわち
\[2x\equiv 6\:(\mathrm{mod}\;7)\]
の解は（両辺の数字が等しければもちろん合同なので）、乗算表を用いなくても $x\equiv 3\:(\mathrm{mod}\;7)$ であることがわかりそうな気がします。$\mathrm{mod}\;7$ においてはそうしても構わないのですが、一般的にはこのような解き方ができるのかどうか注意する必要があります。というのは、$C_3$ 以外に方程式を満たす解が存在する可能性があるからです。

乗算表を眺めると、$\mathrm{mod}\;7$ においては各行・各列で重なっている数字、欠けている数字がないので、全ての類同士で割り算が可能であることがわかります。そういう点で $\mathrm{mod}\;7$ はとても性質が良くて扱いやすい法なのです。しかし法の選び方によっては、合同方程式の解が常があるとは限らないし、また解がひとつの類に定まらないこともあります。

6 を法とする合同方程式

　$6$ を法とする合同方程式を考えてみます。$\mathrm{mod}\;6$ の乗算表は次のようになります。



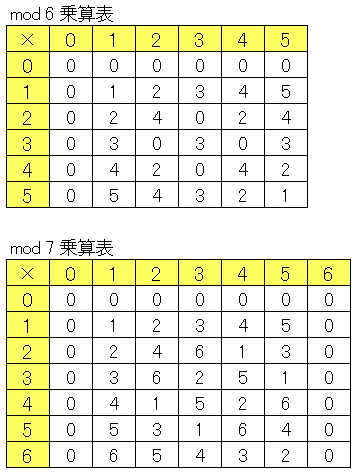
比較のために $\mathrm{mod}\;7$ 乗算表も再掲しています。$\mathrm{mod}\;7$ 乗算表の各行では $0$ から $6$ の数字が一通り現れていますが、$\mathrm{mod}\;6$ 乗算表では同じ数が周期的に現れる行が存在しています。するとたとえば
\[2x\equiv 4\:(\mathrm{mod}\;6)\]
という合同方程式は

\[x\equiv 2,\:5\:(\mathrm{mod}\;6)\]
という複数の解をもつことになります。



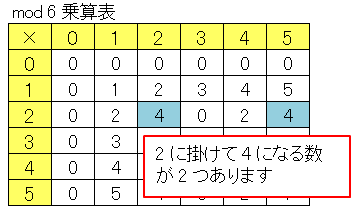
また $2x\equiv 5\:(\mathrm{mod}\;6)$ という合同方程式を解こうとしても、$2$ に乗じて $5$ になるような数は乗算表のどこにも見当たらないので「解なし」ということになります。このように合同方程式では、選んだ法によって解が存在しなかったり不定であったりする場合があるのですが、そこにはもちろん法則があるので、これから丁寧に調べていきます。

合同式の両辺を割ることのできる条件

そこでまず普通の等式と同じように合同式の両辺を同じ数で割ってもよいのかどうかを考えます。先ほどの例の
\[2x\equiv 4\:(\mathrm{mod}\;6)\]
という合同方程式で両辺を $2$ で割って
\[x\equiv 2\:(\mathrm{mod}\;6)\]
としてしまうと 2 つあるうちの一方の解しか得られないので明らかに誤りです。しかし法を $7$ に変えて
\[2x\equiv 4\:(\mathrm{mod}\;7)\]
という合同方程式であれば、
\[x\equiv 2\:(\mathrm{mod}\;7)\]
として全く問題ありません。選んだ法によって、どうしてこのような違いが生じてしまうのでしょう。それについて述べているのが次の定理です。

【証明】証明には以前に学んだ定理 A11

\[(a,\:b)=1,\quad a\:|\:bc\quad \Longrightarrow\quad a\:|\:c\]
を用います。$ca\equiv cb\:(\mathrm{mod}\;m)$ なので、
\[m\:|\:c(a-b)\]
$(c,\:m)=1$ のときは定理 A11 より
\[m\:|\:a-b\quad\therefore a\equiv b\:(\mathrm{mod}\;m)\]
$(c,\:m)=d\gt 1$ のとき
\[c=dc’,\quad m=dm’\]
とおくと $(c’,\:m’)=1$ なので
\[\begin{align*}dm’&\:|\:dc'(a-b)\:(\mathrm{mod}\;m)\\[6pt]m’&\:|\:c'(a-b)\:(\mathrm{mod}\;m)\\[6pt]m’&\:|\:a-b\:(\mathrm{mod}\;m)\\[6pt]&\therefore a\equiv b\:(\mathrm{mod}\;m)\end{align*}\]
となります。（証明終）

この定理は $c$ と $m$ が互いに素である場合のみ、両辺を $c$ で割っても合同関係が維持されることを述べています（互いに素でなければ法を $m/d$ に変えて合同式が成り立ちます）。再び先ほどの
\[2x\equiv 4\:(\mathrm{mod}\;6)\]
という合同方程式を考えると、
\[(c,\:m)=(2,\:6)\neq 1\]
なので両辺を $2$ で割ることはできません。しかし
\[2x\equiv 4\:(\mathrm{mod}\;7)\]
であれば、
\[(c,\:m)=(2,\:7)=1\]
ですから、両辺を $2$ で割って
\[x\equiv 2\:(\mathrm{mod}\;7)\]
とすることができます。一般に
\[cx\equiv ca\:(\mathrm{mod}\;m)\]
という合同方程式を考えたときに、$m$ が素数でれば、どのような $c$ とも互いに素な関係にあるので、合同方程式の両辺を $c$ で割ることができます。一方で $m$ が合成数であるときは、$m$ と互いに素ではない $c$ については、合同方程式の両辺を $c$ で割ることはできないのです。

n元一次不定方程式の定義

乗算表を用いれば一次合同方程式は簡単に解けますが、現実的には法が小さい場合にのみ有効な方法です。たとえば $\mathrm{mod}\;123$ の乗算表を作ろうと考える人はさすがにいないでしょう。そこで、これからしばらくは一次合同方程式
\[ax\equiv b\:(\mathrm{mod}\;m)\]
の一般的な解法を調べていくことにします。上式は
\[ax-b\:|\:m\]
を意味するので、整数 $y$ を導入すると
\[ax-b=my\quad\Longleftrightarrow\quad ax-my=b\]
と表せるので、一次合同方程式とは二元一次不定方程式に他ならないということになります。まずは不定方程式の定義を載せておきます。

ちなみに n元一次不定方程式を英語で書くと linear indeterminate equation with n-unknowns です。または古代アレクサンドリアの数学者ディオファントスにちなんでディオファントスの不定方程式とよばれることもあります。

不定方程式 ax + by = (a, b)

まず最初に次のような二元一次不定方程式
\[ax+by=g=(a,\:b)\]
を考えます。すなわち定数項が係数 $a,\:b$ の最大公約数となっているという極めて特殊な形の不定方程式ですが、この方程式には必ず整数解が存在するという定理が合同方程式を解くための重要な鍵となります。

【証明】本講座の序盤で学んだユークリッドの互除法を用いて証明します。
$a=a_1,\:\:b=a_2$ とおくと、
\[\begin{align*}&a_1=a_2\,q_1+a_3\quad (0\leq a_3\lt a_2)\quad\quad (1)\\[6pt]&a_2=a_3\,q_2+a_4\quad (0\leq a_4\lt a_3)\quad\quad (2)\\[6pt]&a_3=a_4\,q_3+a_5\quad (0\leq a_5\lt a_4)\quad\quad (3)\\[6pt]&\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\\[6pt]&a_{n-1}=a_n\,q_{n-1}+a_{n+1}\quad (0\leq a_{n+1}\lt a_n)\\[6pt]&a_n=a_{n+1}q_n\end{align*}\]
のように表せて、$a_{n+1}$ が $a_1$ と $a_2$ の最大公約数になります：
\[(a_1,\:a_2)=(a_2,\:a_3)=(a_3,\:a_4)=\:\cdots\:=(a_n,\:a_{n+1})=a_{n+1}\]
すなわち $g=a_{n+1}$ となります。(1) より
\[a_3=a_1-a_2\,q_1\tag{4}\]
を (2) に代入すると
\[a_4=-a_1\,q_2+a_2\,(1+q_1\,q_2)\tag{5}\]
(4) と (5) を (3) に代入すると
\[a_5=a_1\,(1+q_2\,q_3)-a_2\,(q_1+q_3+q_1\,q_2\,q_3)\]
となります。これを繰り返していけば、$a_{n+1}$ も $a_1$ と $a_2$ で表すことができます。すなわち
\[a_{n+1}=a_1\,x+a_2\,y\:\:(x\in\mathbb{Z},\:y\in\mathbb{Z})\]
したがって $ax+by=c$ を満たす解が必ず存在します。（証明終）

定理 C6 はいわゆる存在定理なのですが、その証明自体が具体的に解を求める手順になっています。この方法によって 1 組の解は求められますが、それを用いて不定方程式の一般的な解を得るためには以下の定理を用います。

[証明] $x_0,\:y_0$ は方程式の解なので、
\[\begin{align*}ax+by=g\\[6pt]ax_0+by_0=g\end{align*}\]
が成り立ちます。両辺を差し引いて
\[a(x-x_0)+b(y-y_0)=0\]
$a=ga’,\:b=gb’$ を代入すると
\[a'(x-x_0)+b'(y-y_0)=0\]
$(a’,\:b’)=1$ より、$b\:|\:x-x_0$ なので
\[\begin{align*}&x-x_0=b’k,\quad y-y_0=-a’k\\[6pt]&\therefore x=x_0+b’k,\quad y=y_0-a’k\end{align*}\]
ごく簡単な例をひとつだけ載せておきます。
\[35x+19y=1\]
ユークリッドの互除法より
\[\begin{align*}35&=19\times 1+16\\[6pt]19&=16\times 1+3\\[6pt]16&=3\times 5+1\end{align*}\]
つまり $35$ と $19$ は互いに素（最大公約数が $1$）となっています。
$a=35,\:b=19$ とおいて上の式を書き直すと
\[\begin{align*}a&=b+16\quad\quad (1)\\[6pt]b&=16+3\quad\quad (2)\\[6pt]16&=3\times 5+1\quad\quad (3)\end{align*}\]
(1) より $16=a-b$ を (2) に代入すると
\[3=2b-a\quad\quad (4)\]
$16=a-b$ と (4) を (3) に代入して
\[6a-11b=1\]
したがって
\[x_0=6,\quad y_0=-11\]
という 1 組の解が得られます。定理 C7 より一般解は
\[x=6+19k,\quad y=-11-35k\]
となります。

不定方程式 ax + by = c が解をもつ条件

定理 C6 では右辺が $a,\:b$ の最大公約数のときに解をもつというものでしたが、この条件はもう少しだけ緩めることができます。

【証明】
まずは必要条件を示します。
$ax+by=c$ が整数解 $x,\:y$ をもつとき、$ax+by$ は整数となります。
\[(a,\;b)\:|\:a,\quad (a,\;b)\:|\:b\]
なので、定理 A3 より
\[(a,\;b)\:|\:ax+by\]
すなわち $(a,\:b)\:|\:c$ となります。

次は十分条件を示します。
$(a,\:b)\:|\:c$ が成り立っているとき、$(a,\:b)=g$ とおくと定理 C6 より
\[ax’+by’=g\]
を満たす $x’,\:y’$ が存在しています。また、$(a,\:b)\:|\:c$ なので $c=gc’$ となるような $c’$ も存在します。そこで上の式に $c’$ を掛けると
\[\begin{align*}ax’c’+by’c’=gc’\\[6pt]
a(c’x’)+b(c’y’)=c\end{align*}\]
となって、$x=c’x’,\;y=c’y’$ という解が存在します。（証明終）

aとmが互いに素である方程式に帰着

一元一次合同方程式と二元一次不定方程式は同等であって、その表現の仕方が異なるだけです。今回は前回までに得た定理等を用いて合同式による表現を見ていきます。まずは次の定理を証明します。

【証明】$ax\equiv b\:\:(\mathrm{mod}\;m)$ なので
\[ax-b=my\:\:(y\in\mathbb{Z})\]
と表せます。すなわち
\[ax-my=b\tag{1}\]
となるので、前回記事の定理 C8

より、$(a,\;m)\:|\:b$ のときに限って解をもちます。また、
\[(a,\:m)=g,\:\:a=a’g,\:\:b=b’g,\:\:m=m’g\]
とおいて (1) に代入すると
\[a’x-m’y=b’\]
となるので、
\[a’x\equiv b’\:\:(\mathrm{mod}\;m’)\]
を解くことに帰着します。（証明終）

この定理は全ての一元一次合同方程式が $(a’,\;m’)=1$ すなわち $a’$ と $m’$ が互いに素となるような方程式に帰着できることを示しています。したがって、$(a,\;m)=1$ となるような合同方程式の解き方を知ることができれば、全ての一元一次合同方程式を解くことができるようになるということです。

一元一次合同方程式の解の個数

$(a,\;m)=1$ であれば解は１つ、そうでなければ $g$ 個の解をもつ、ということを述べているのが次の定理です。

【証明】$g\:|\:b$ のときに限って解をもつことは【定理9】で証明しました。

(1) $ax\equiv b\:\:(\mathrm{mod}\;m)$ より
\[ax-my=b\:\:(y\in\mathbb{Z})\]
と表せます。$(a,\;m)=1$ なので 定理 C8

によって、この方程式には整数解が存在するので、それを $x_0$ とおくと一般解は
\[x=x_0+km\:\:(y\in\mathbb{Z})\]
と表すことができます。したがって
\[x\equiv x_0\:\:(\mathrm{mod}\;m)\]
となり、合同方程式の解は全て同じ剰余類に属することになります。

(2) $g\:|\:b$ なので、【定理C8】より $ax\equiv b\:\:(\mathrm{mod}\;m)$ は解をもちます。その中の解の１つを $x_0$ , 一般解を $x$ とすると
\[\begin{cases}ax\equiv b & (\mathrm{mod}\;m)\\[6pt]ax_0\equiv b & (\mathrm{mod}\;m)\end{cases}\]
なので、
\[ax\equiv ax_0\:\:(\mathrm{mod}\;m)\]
が成り立ちます。ここで以前に証明した定理 C5

を用いると、
\[x\equiv x_0\:\left(\mathrm{mod}\;\displaystyle\frac{m}{g}\right)\]
が成り立つことがわかります。したがって
\[x=x_0+k\:\frac{m}{g}\]
と表せますが、$\mathrm{mod}\;m$ で相異なる解となるのは
\[k=0,\;1,\:\cdots ,\:m-1\]
のときです ($k=0$ と $k=m$ は同じ類に属します)。よって解の個数は $g$ 個あり、その解は
\[x=x_0+k\:\frac{m}{g}\:\:(k=0,\;1,\:\cdots ,\:m-1)\]
で与えられます。（証明終）

一元一次合同方程式の具体例

簡単な合同方程式を解いてみます。
\[26x\equiv 30\:\:(\mathrm{mod}\;8)\tag{1}\]
$g=(a,\;m)=(26,\;8)=2$ なので、
\[13x\equiv 15\:\:(\mathrm{mod}\;4)\tag{2}\]
という合同方程式に帰着します。ここで
\[4x\equiv 4\:\:(\mathrm{mod}\;4)\tag{3}\]
という合同式は当然成り立つので、(2) から (3) × 3 を引いて
\[x\equiv 3\:\:(\mathrm{mod}\;4)\]
という１つの解を得ます。これを $x_0$ とすると一般解は
\[x=x_0+k\:\frac{m}{g}\:\:(k=0,\;1,\:\cdots ,\:m-1)\]
で与えられます。$m/g=8/2=4$ なので $\mathrm{mod}\;8$ では
\[x\equiv 3,\:\:7\:\:(\mathrm{mod}\;8)\]
となります。これは剰余類 $C_3$ の要素 $x=3+8k$、および剰余類 $C_7$ の要素 $x=7+8k$ が全て $26x\equiv 30\:\:(\mathrm{mod}\;8)$ を満たすということです。