コーシー・シュワルツの不等式

コーシー・シュワルツの不等式

任意の実数 $a_i, b_i$ について
 \[\left(\sum_{i=1}^{n}a_ib_i\right)^2\leq\left(\sum_{i=1}^{n}a_i^2\right)\left(\sum_{i=1}^{n}b_i^2\right )\tag{1}\]
が成立します。等号は
 \[a_1:a_2:\:\cdots\::a_n=b_1:b_2:\:\cdots\::b_n\]
のときに成り立ちます。この関係を シュワルツの不等式 (Schwarz’s inequality)、またはコーシー・シュワルツの不等式とよびます。$n=2$ であれば
 \[(a_1b_1+a_2b_2)^2\leq (a_1^2+a_2^2)\:(b_1^2+b_2^2)\tag{2}\]
と書けます。

コーシー・シュワルツの不等式の証明

まずは $n=2$ の場合について証明してみます。一次式の平方の和について
 \[(a_1x-b_1)^2+(a_2x-b_2)^2\geq 0\]
は常に成り立っています。展開して整理すると
 \[(a_1^2x+a_2^2)\:x^2-2(a_1b_1+a_2b_2)\:x+b_1^2+b_2^2\geq 0\]
左辺を $f(x)$ とおくと、$f(x)\geq 0$ が常に成り立っているということは、二次方程式 $f(x)=0$ において判別式 $D/4$ が $0$ 以下であるということです。つまりグラフで見たときに $f(x)$ が $x$ 軸と全く交わらないか、ただ $1$ 点のみで接する状態です。したがって
 \[\frac{D}{4}=(a_1b_1+a_2b_2)^2-(a_1^2+a_2^2)(b_1^2+b_2^2)\leq 0\]
となり、
 \[(a_1b_1+a_2b_2)^2 \leq (a_1^2+a_2^2)(b_1^2+b_2^2)\tag{2}\]
が恒等的に成り立つことがわかります。等号が成立するのは
 \[(a_1x-b_1)^2+(a_2x-b_2)^2=0\]
のとき、すなわち
 \[a_1x-b_1=0,\quad a_2x-b_2=0\]
のときですから、$a_1\neq 0,\:a_2\neq 0$ のときは
 \[\frac{b_1}{a_1}=\frac{b_2}{a_2}\]
となります。ただし $a_1=0$ であれば $b_1=0$ でなければならず、このとき
 \[a_1:a_2 =0:a_2\]
のように書くことを約束しておけば、$a_1$ 或いは $a_2$ が $0$ であるかないかに関わらず等号成立条件を
 \[a_1:a_2=b_1:b_2\]
と比例関係で表すことができます（証明終）。

一般の $n$ についてのシュワルツの不等式も同じように証明できます。一次式の平方の和について
 \[\sum_{i=1}^{n}(a_ix-b_i)^2\geq 0\]
が成り立ちます。展開して整理すると
 \[\left(\sum_{i=1}^{n}a_i^2\right )x^2-2\left(\sum_{i=1}^{n}a_i\:b_i\right )x+\left(\sum_{i=1}^{n}b_i^2\right)\geq 0\]
この式を満たすのは判別式 $D/4$ が $0$ 以下のときなので
 \[\frac{D}{4}=\left(\sum_{i=1}^{n}a_i\:b_i\right )^2-\left(\sum_{i=1}^{n}a_i^2\right)\left(\sum_{i=1}^{n}a_i^2\right)\leq 0\]
したがって
 \[\left(\sum_{i=1}^{n}a_ib_i\right)^2\leq\left(\sum_{i=1}^{n}a_i^2\right)\left(\sum_{i=1}^{n}b_i^2\right )\tag{1}\]
が成立します。等号が成立するのは
 \[\sum_{i=1}^{n}(a_ix-b_i)^2=0\]
のとき、すなわち全ての i について
 \[a_ix-b_i=0\]
を満たすときだけです。$a_i\neq 0$ である場合に限って
 \[\frac{b_1}{a_1}=\frac{b_2}{a_2}=\cdots\frac{b_n}{a_n}\]
と書くことができます。これは
 \[a_1:a_2:\:\cdots\::a_n=b_1:b_2:\:\cdots\::b_n\]
と同値です。ただし $a_i=0$ であれば \(b_i=0\) ですが、$0$ に対しては $0$ を対応させるという約束のもとで、上記の比例式にまとめることができます（証明終）。

コーシー・シュワルツの不等式をベクトルでイメージします

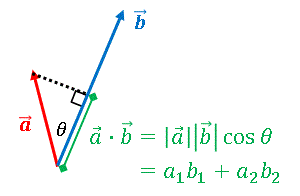$n=2,\:3$ の場合はベクトルでシュワルツの不等式の本質を理解することができます。ここでは簡単のために平面上の 2 つのベクトルの内積を考えます。内積の定義により
 \[\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta\]
ですから、両辺を $2$ 乗すると
 \[(\vec{a}\cdot\vec{b})^2=|\vec{a}|^2|\vec{b}|^2\cos^2\theta\]
$0\leq\cos^2\theta\leq 1$ なので、
 \[(\vec{a}\cdot\vec{b})^2\leq |\vec{a}|^2|\vec{b}|^2\]
が成り立ちます。成分表示すればこれはシュワルツの不等式そのものです。
 \[(a_1b_1+a_2b_2)^2\leq (a_1^2+a_2^2)(b_1^2+b_2^2)\]
等号が成立するのは $\cos^2\theta=1$ のとき、つまり 2 つのベクトルが平行になるときです。それは
 \[\vec{a}=k\vec{b}\]
が成立するときで、各ベクトルの成分は
 \[a_1=kb_1,\quad a_2=kb_2\]
と書くことができますから、
 \[\frac{a_1}{b_1}=\frac{a_2}{b_2}\]
が等号成立の条件となります。

コーシー・シュワルツの不等式の感覚を掴みます

見やすいように実数 $a,\:b,\:c,\:d$ を使ってシュワルツの不等式を書き直しておきます。
 \[(ac+bd)^2\leq (a^2+b^2)(c^2+d^2)\]
等号成立条件は $a:b=c:d$ ですから、$a:b\simeq c:d$ であれば微妙な大小関係を判定をしてくれるということです。ベクトル形式でいえば、$\theta\simeq 0$ のところです。さらに簡単にするために $b=d=1$ とおくと
 \[(ac+1)^2\leq (a^2+1)(c^2+1)\]
という不等式になります。そこでたとえば $a=10,\:c=11$ としてみると
 \[左辺\:=12321\quad 右辺\:=12322\]
となって、その差はわずかに $1$ です！

コーシー・シュワルツの不等式と相加相乗平均と組み合わせてみます

$a,\:b,\:c,\:d$ で表したシュワルツの不等式
 \[(ac+bd)^2\leq (a^2+b^2)(c^2+d^2)\]
において $c=d=1$ とおくと
 \[\frac{(a+b)^2}{4}\leq\frac{a^2+b^2}{2}\]
となります。一方で相加・相乗平均の関係によると
 \[\sqrt{ab}\leq\frac{a+b}{2}\]
となっています。両辺を 2 乗すると
 \[ab\leq\left(\frac{a+b}{2}\right)^2\]
となります。さきほどの不等式を組合わせると
 \[ab\leq\left(\frac{a+b}{2}\right)^2\leq\frac{a^2+b^2}{2}\]
という不等式を得ることができます。たとえば $a=2,\:b=1$ としてみると
 \[\frac{8}{4}\leq\frac{9}{4}\leq\frac{10}{4}\]
という関係を表しています。