バーンスレイのシダ
任意の大きさの断片を切り取ったとき、図形全体の形状と相似になっているような構造をフラクタルとよびます。その代表例の1つとして、英国の数学者マイケル・バーンスレイ(Micael Barnsley)によって発見されたバーンスレイのシダ(Barnsley fern)という図形があります。
バーンスレイのシダとは、以下のような規則で人工的にシダの形状をコンピュータ上に再現するものです。
・$(x_0,\ y_0)=(0,\ 0)$ を始点に設定
・確率的に変換 A ~ D を繰り返し選択して次の座標を決定
変換 A (確率 $0.01$)
$x_{n+1}=0$
$y_{n+1}=0.16y_n$
変換 B (確率 $0.07$)
$x_{n+1}=-0.15x_n+0.28y_n$
$y_{n+1}=0.26x_n+0.24y_n+0.44$
変換 C (確率 $0.07$)
$x_{n+1}=0.2x_n-0.26y_n$
$y_{n+1}=0.23x_n+0.22y_n+1.6$
変換 D (確率 $0.85$)
$x_{n+1}=0.85x_n+0.04y_n$
$y_{n+1}=-0.04x_n+0.85y_n+1.6$
以下コードで、アクティブなワークシートの A 列と B 列に1000 点のシダの座標を作成します。
'[VBA] バーンスレイのシダ (Barnsley fern) Option Base 0 Sub Barnsley_fern() Dim x() As Double Dim y() As Double Dim rd As Double Dim j As Long, k As Long, pt As Long '配列インデクスの上限値 pt = 999 '空の配列を生成 ReDim x(pt), y(pt) '初期値の設定 x(0) = 0 y(0) = 0 '乱数を初期化 Randomize (10) 'バーンスレイのシダをプロット For j = 1 To pt rd = Rnd() Select Case rd Case 0 To 0.01 x(j) = 0 y(j) = 0.16 * y(j - 1) Case 0.01 To 0.07 x(j) = -0.15 * x(j - 1) + 0.28 * y(j - 1) y(j) = 0.26 * x(j - 1) + 0.24 * y(j - 1) + 0.44 Case 0.07 To 0.14 x(j) = 0.2 * x(j - 1) - 0.26 * y(j - 1) y(j) = 0.23 * x(j - 1) + 0.22 * y(j - 1) + 1.6 Case Else x(j) = 0.85 * x(j - 1) + 0.04 * y(j - 1) y(j) = -0.04 * x(j - 1) + 0.85 * y(j - 1) + 1.6 End Select Next j 'データの見出しを入力 Cells(1, 1) = "x" Cells(1, 2) = "y" 'ワークシートにデータを転記 For k = 0 To pt Cells(k + 2, 1) = x(k) Cells(k + 2, 2) = y(k) Next k End Sub
Barnsley_fern() を実行すると、下図のようにシートにデータが作成されます。
[挿入]タブから散布図を作成してください(マーカーの色やサイズなどは適当に調整してください)。次のような図が表示されます。
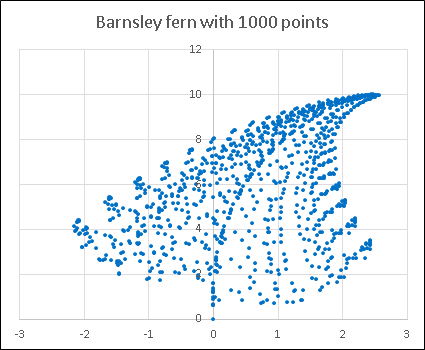
コードの pt を変更すると絵の密度を変えることができます。
下の図は pt = 4999 として、5000 点で描いたシダの絵です。
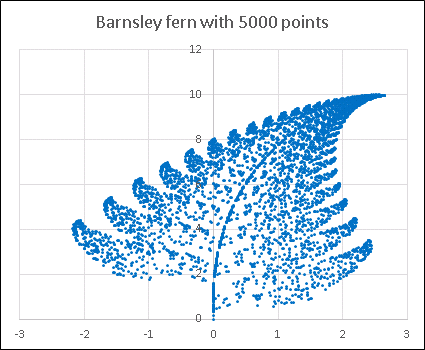
エクセルや数学に関するコメントをお寄せください
Blog Catのテストコメントです。ついでに何か数学の雑談でも書こうかと思いましたけど、特に何も思いつきませんね … これから買い物に出かけてペンネを買おうかな、もう明日でいいかなと悩んでます。