【Excel】微分方程式の数値解の求め方

【Excel】常微分方程式の数値解

微分方程式の数値解を計算するための初等的なメソッドの一つに、オイラー法があります。オイラー法とは、ある関数 $y=f(x)$ について次のような形をした微分方程式を解くために用いられる手法です。
 \[\frac{dy}{dx}=F(x,y)\]
右辺は $x$ と $y$ の 2 変数関数（もちろん 1 変数でも構わない）なので、かなり幅広い種類の微分方程式を含むことになります。$x$ から少しだけ離れた $x+\Delta x$ における $y$ の値をテイラー展開の最初の 2 項をとって
 \[f(x+\Delta x)=f(x)+f’ (x)\Delta x\]
と近似します。$f’ (x)=F(x,y)$ なので
 \[f(x+\Delta x)=f(x)+F(x,y)\Delta x\]
と書き直せます。初期値 $(x_0,y_0)$ を与えて、そこから少しだけずれた点の $f(x_1)$ を求め、さらにその値をもとに $f(x_2),f(x_3),\cdots$ を計算していけば、$x$ と $y$ のデータが得られます。

例として、微分方程式
 \[\frac{dy}{dx}=x(1-y)\]
の数値解を求めてみましょう。オイラー法では
 \[f(x+\Delta x)=f(x)+x(1-y)\Delta x\]
で近似計算することになります。まず下図のようなシートを作ります。
 

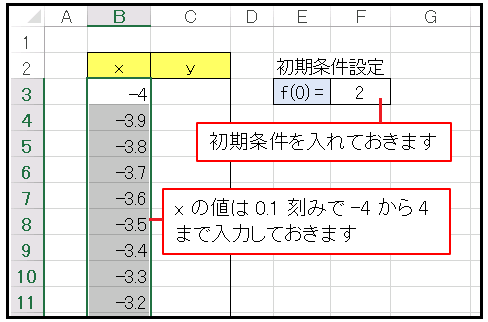
$\Delta x=0.1$ に設定します。$x$ の値を 0.1 刻みで－4 から 4 まで入力してください。また $x=0$ における $y=f(x)$ の値、すなわち $f(0)$ を 2 としておきます。この $x=0$ の値を基準に順次オイラー法で値を入れるのですが、$x$ が増加する方向では $\Delta x$ が正、すなわち + 0.1 ですが、$x$ が減少する方向では $\Delta x$ は負、すなわち －0.1 となることに注意して、数式を書き分ける必要があります。
 

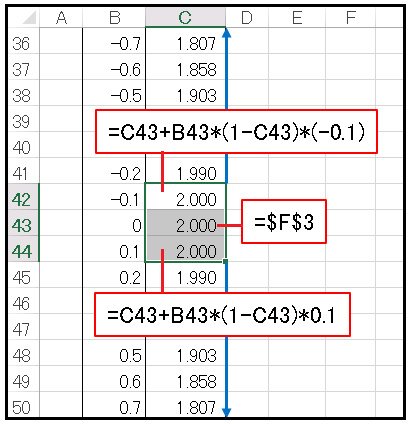
セル C43 には先ほど記入しておいたセル F3 の初期条件を絶対参照して

=$F$3

と入力します。セル C42 には

=C43+B43*(1-C43)*(-0.1)

という数式を入れてセル C3 までコピーします。セル C44 には

=C43+B43*(1-C43)*0.1

と入力し、右下隅をダブルクリックして行末まで数値を埋めます。入力されたデータ範囲を選択して [挿入] 、[散布図] 、[散布図] の順に選択すると次のようなグラフが表示されるはずです。
 

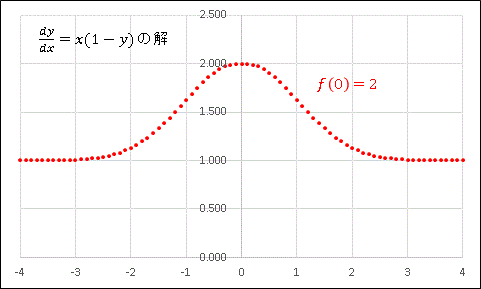
$(0,f(0))$ を頂点として正負の方向に減衰する関数です。しかし初期値のとりかたによって、グラフの形（解曲線）は大きく変化します。今度は $f(0)=0$ としてみましょう。
 

今度は $(0,f(0))$ が谷底となるグラフです。
次は初期値を $f(0)=1$ としてみると…
 

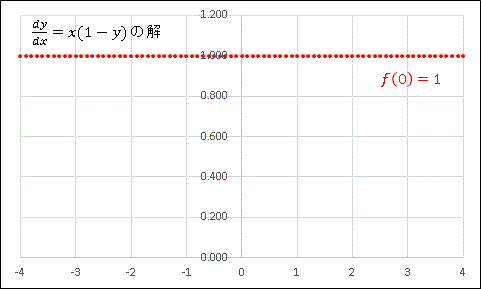
$y=1$ という直線になってしまいます (いわゆる特解です)。
この微分方程式の理論解は初期値を用いて
 \[y=1+(f(0)-1)\exp\left(-\frac{x^2}{2}\right)\]
と表せて、$f(0)=1$ を境に解曲線を 2 つの群に分けることが知られています。変数分離で簡単に解けるので、気になる人は試してみてください。
 
≫ Pythonのサイトでもオイラー法による数値解を扱っています