上に有界な単調増加数列は収束します

数列の有界性

すべての $n$ について $a_n\le c$ となる実数 $c$ が存在するとき、数列 $\{a_n\}$ は上に有界であるといいます。また $c$ を上界（upper bound）といいます。すべての $n$ について $b\le a_n$ となる実数 $b$ が存在するとき、数列 $\{a_n\}$ は 下に有界 であるといいます。また $b$ を下界（lower bound）といいます。数列 $\{a_n\}$ が上に有界であり、なおかつ下に有界であるとき、つまりすべての $n$ について $b\le a_n\le c$ が成り立っているとき、数列 $\{a_n\}$ は有界であるといいます。

数の集合 $A$ について上界の中で最小のものを 上限（supremum）とよんで $\sup A$ と表します。また下界の中で最大のものを下限（infimum）とよんで $\inf A$ と表します。集合 $A$ が数列 $\{a_n\}$ であるときは上限を $\sup \{a_n|n\in \mathbb{N}\}$ のように書くこともあります。

有界数列の例として、$a_n=1-1/n$ で表される数列を考えてみます。この数列は下の図にあるように $0\le a_n<1$ の範囲に存在しています。
 

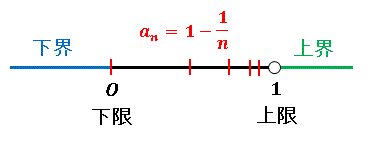
つまりこの数列は有界であり、0 以下の実数はすべて下界となります（青い部分）。そのなかの最大値が 0 であり、これが下限です。また 1 以上の実数はすべて上界です（緑の部分）。1 より僅かでも小さな値 $1-\epsilon$ は上界になりえません。なぜなら $n\to \mathrm{\infty }$ で $\{a_n\}$ は $1-\epsilon$ を追い越していくらでも 1 に近づくことができるからです。上界の最小値は 1 であり、これが上限となります。

実数の連続性

上限と下限について、以下のような実数の連続性の公理が与えられています。

公理の内容を図で示すと次のようになります。
 

（上にも下にも）有界な部分集合 $A$ をとると、公理は $\sup A$ と $\inf A$ が存在することを示しています。

単調増加数列と単調減少数列は収束します

任意の $n$ について $a_n\le a_{n+1}$ が成り立つ数列 $\{a_n\}$ を単調増加数列とよび、上に有界な単調増加数列は必ず収束します。

【$a_n=1-1/n$ が収束することの証明】
いきなり定理の一般的な証明にかかるとイメージしにくいので、まず先ほど例にあげた単調増加数列 $a_n=1-1/n$ が収束することを証明してみます。図も再掲しておきます。
 

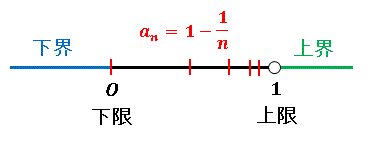
$A=\{a_n|n\in \mathbb{N}\}$ とおきます。上限 $\sup A$ が存在して、その値は 1 です。つまりすべての $n$ について $a_n<1$ が成り立ちます。上限 $\sup A$ は上界の最小値ですから、どのような $1-\epsilon$ も $A$ の上界とはなりえません。つまり $1-\epsilon <a_k$ となる $k$ が存在して、$n>k$ のとき
 $$1-\epsilon <a_k\le a_n<1$$
を満たしています。これが任意の $\epsilon$ について成り立っているわけですから、$a_n$ は 1 に収束します。

【単調増加数列が収束することの証明】
同じように全ての単調増加数列が収束することを証明します。
$A=\{a_n|n\in \mathbb{R}\}$ とおきます。上限 $u=\sup A$ が存在します。つまりすべての $n$ について $a_n\le u$ が成り立ちます。上限 $u$ は上界の最小値なので、どのような $u-\epsilon$ も $A$ の上界ではありません。すなわち $u-\epsilon <a_k$ となる $k$ が存在して、$n>k$ のとき
 $$u-\epsilon <a_k\le a_n\le u$$
を満たしています。これが任意の $\epsilon$ について成り立つので $a_n$ は $u$ に収束します。