チェビシェフの不等式で分布のばらつきを調べる

チェビシェフの不等式

分散または標準偏差は分布のばらつきを表していますが、それが具体的にどの程度なのかということを、チェビシェフの不等式 (Chebyshev’s inequality)
 \[\begin{align*}
P(|x-\mu|\geq k\sigma)&\leq\frac{1}{k^2}\tag{A}\\[6pt]P(|x-\mu|\lt k\sigma)&\geq 1-\frac{1}{k^2}\tag{B}\end{align*}\]
によって知ることができます。ここで、$k$ は任意実数、$\mu$ は期待値、$\sigma$ は標準偏差です。

不等式(A) の意味するところを具体的に書き並べてみると
\[\begin{align*}&平均から\,2\sigma\,以上離れている確率\,\leq\frac{1}{4}\\[6pt]&平均から\,3\sigma\,以上離れている確率\,\leq\frac{1}{9}\\[6pt]&平均から\,4\sigma\,以上離れている確率\,\leq\frac{1}{16}\end{align*}\]
のようになります。

チェビシェフの不等式の証明

チェビシェフの不等式を証明しておきます。最初に不等式(A)について、$X$ が離散確率変数の場合と、連続変数の場合に分けて証明します。

【離散確率変数の場合】確率変数が離散変数であるときの分散は
 \[\sigma^2=\sum_{i=1}^{n}(x_i-\mu)^2f(x_i)\]
と定義されています。ここで右辺の和の各項は全て正なので、$|x_i-\mu|\geq k\sigma$ となる部分だけを取り出せば
 \[\sigma^2\geq\sum_{|x_i-\mu|\geq k\sigma}(x_i-\mu)^2f(x_i)\]
という不等式が成り立ちます。$|x_i-\mu|\geq k\sigma$ の範囲では明らかに $(x_i-\mu)^2\geq k^2\sigma^2$ が成り立っているので、
 \[\sigma^2\geq\sum_{|x_i-\mu|\geq k\sigma}k^2\sigma^2f(x_i)=k^2\sigma^2P(|x-\mu|\geq k\sigma)\]
すなわち
 \[P(|x-\mu|\geq k\sigma)\leq\frac{1}{k^2}\]
となります。

【連続確率変数の場合】確率変数が連続変数であるときの分散は
 \[\sigma^2=\int_{-\infty}^{\infty}(x-\mu)^2f(x)dx\]
という積分で定義されます。被積分関数は常に正なので、$\mu-k\sigma\leq x\leq \mu+k\sigma$ の範囲の積分を抜き取ってしまって
 \[\sigma^2\geq\int_{-\infty}^{\mu-k\sigma}(x-\mu)^2f(x)dx+\int_{\mu+k\sigma}^{\infty}(x-\mu)^2f(x)dx\]
という不等式をつくります。$x\leq\mu-k\sigma$ および $x\geq\mu+k\sigma$ の範囲では $(x-\mu)^2\geq 0$ なので、
 \[\begin{align*}\sigma^2&\geq k^2\sigma^2\left\{ \int_{-\infty}^{\mu-k\sigma}(x-\mu)^2f(x)dx+\int_{\mu+k\sigma}^{\infty}(x-\mu)^2f(x)dx\right\}\\[6pt]&=k^2\sigma^2\left\{ P(X\leq\mu-k\sigma)+P(X\geq\mu+k\sigma)\right\}\\[6pt]&=k^2\sigma^2P(|x-\mu|\geq k\sigma)\end{align*}\]
となって、やはり同じ不等式
 \[P(|x-\mu|\geq k\sigma)\leq\frac{1}{k^2}\]
を得ることができます。

次に不等式(B)を証明します。(A) の左辺は
 \[P(|x-\mu|\geq k\sigma)=1-P(|x-\mu|\lt k\sigma)\]
と書き換えられるので、
 \[P(|x-\mu|\lt k\sigma)\geq 1-\frac{1}{k^2}\tag{B}\]
が成り立つことがわかります。

【Excel】チェビシェフの不等式

例として平均値 $60$, 標準偏差 $5$ の正規分布でチェビシェフの不等式が成り立っていることを調べてみます。
 

 
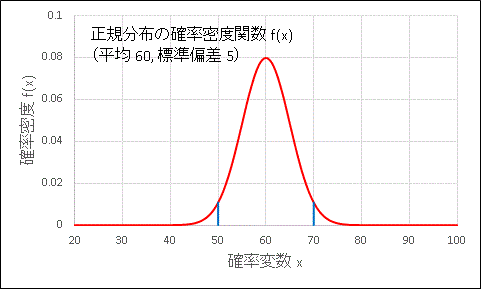
上の図は正規分布の確率密度 $f(x)$ のグラフです。正規分布は平均値 $x=\mu$ について左右対称なので、平均値 $60$ から $2\sigma = 10$ 以上離れている確率は、$f(x)$ を $-\infty$ から 50 まで積分して、確率変数が 50 以下となる確率
\[P(X\leq 50)=F(50)\]を求めて $2$ 倍すればいいことがわかります。ここに $F(x)$ は累積確率分布関数です。Excel では

NORM.DIST(x,平均,標準偏差,関数形式)

において関数形式を 1 として、正規分布の累積確率分布関数を計算することができます。平均値 $60$ から $2\sigma = 10$ 以上離れている確率は

=2*NORM.DIST(50,60,5,1)

として 0.0455 という値を得るので、確かに $1/4=0.25$ より小さくなっていることがわかります。