シッソイド（ディオクレスの疾走線）

シッソイド（疾走線）の描き方

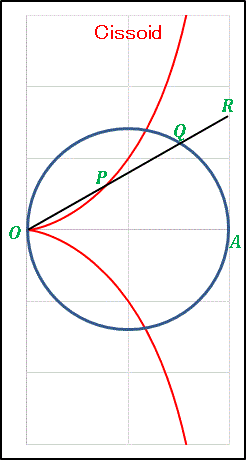　今回はいきなり右側にグラフを載せてしまいますが、赤いラインがシッソイドまたはディオクレスの疾走線と呼ばれるグラフです。ちなみに原語の cissoid は「蔦（つた）の形」という意味です。

図にあるように OA を直径とする円に y 軸と並行となるような接線を引き、O を通る直線と円および接線との交点を Q, R とします。そして OP = QR となるように点 P をとり、R が動くときの P の軌跡が疾走線です。その方程式は円の半径を a として
 \[x^3+(x-a)y^2=0\qquad(a\gt 0)\]
で与えられます。極形式は
 \[r=2a \tan \theta \sin \theta\]
で表され、またパラメータ変数を用いて
 \[x=\frac{at^2}{1+t^2},\quad y=\frac{at^3}{1+t^2}\]
と表すこともできます（右図はこの形式を用いて描かれています）。

非対称葉線

疾走線のパラメータ表示に三角関数を組込んで
 \[x=\frac{t^2\sin t}{1+t^2},\quad 10y=\frac{t^3\sin t}{1+t^2}\]
としてみます（$y$ 軸方向のサイズ調整のために $y$ は $10$ で割ってあります）。
 

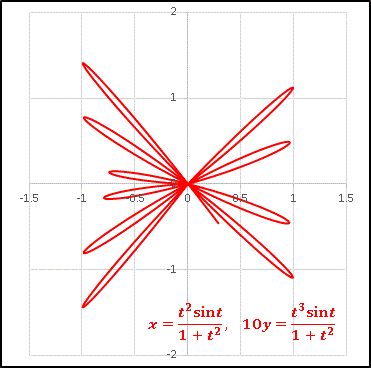
葉のような形が現れましたね。
しかし $x$ 軸に対しても $y$ 軸に対しても微妙に非対称になっています。

不思議な渦巻

上の方程式で $y$ の $\sin{t}$ を $\cos{t}$ に変えて
 \[x=\frac{t^2\sin t}{1+t^2},\quad 10y=\frac{t^3\cos t}{1+t^2}\]
としてみます。
 

 
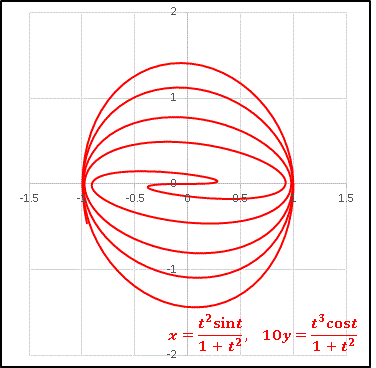
奇妙な渦巻きが現れました。原点で S の字を描くようにして少しずつ外側へ広がってゆきます。