興味深いコメントをいただいたので、記事を見直して大幅に加筆修正しておきました。VBA のコードも改良してあります。
コラッツ予想とコラッツ数列
ある自然数 $n$ から始めて
・$n$ が偶数なら $2$ で割る
・$n$ が奇数なら $3$ をかけて $1$ を加える
このような操作を繰り返すとき、どんな自然数 $n$ に対しても最終的には
\[{1}\rightarrow{4}\rightarrow{2}\rightarrow{1}\]
というループに入る、という主張をコラッツ予想(Collatz Problem)あるいは角谷の問題(Kakutani’s problem)といいます。また、上の規則にしたがって並ぶ数列のことをコラッツ数列とよびます。
たとえば最初の数字を $n=10$ としてコラッツ数列を並べてみると
\[10,\ 5,\ 16,\ 8,\ 4,\ 2,\ 1,\ 4,\ 2,\ 1,\ \cdots\]
となって、確かに最後には $1,\;4,\;2,\;1$ が繰り返されるようになりますね。今度は初期値を $6$ としてみると、
\[6,\ 3,\ 10,\ 5,\ 16,\ 8,\ 4,\ 2,\ 1,\ 4,\ 2,\ 1,\ \cdots\]
やはり $1,\ 4,\ 2,\ 1$ のループに入ってしまいます。
しかし、本当にどんな $n$ についてもこの法則が成り立つのか、ということはまだ証明されていません。もしかすると、この法則を満たさない数が存在しているかもしれないと考えて、計算機を使って巨大数を探索させていますが、いまだに反例も見つかっていません。こういう一見して簡単そうに見える問題ほど、一般的な証明は難しいのです。
コラッツ数列を並べる VBA のプログラム(マクロ)を作っておきました。興味のある人はモジュールにコピーして色々な数字を試してみてください。
'[VBA] コラッツ数列生成サブルーチン
Sub Collatz(n As Long, Optional ws = False)
If n < 2 Then
n = 2
End If
Do Until n < 2
Debug.Print n;
If ws = True Then
ActiveCell = n
ActiveCell.Offset(0, 1).Activate
End If
If n Mod 2 = 0 Then
n = n / 2
Else
n = 3 * n + 1
End If
Loop
Debug.Print 1;
If ws = True Then
ActiveCell = 1
End If
End Sub
引数 n には 2 以上の整数を渡すようにしてください (2 未満の数値を受け取っても自動的に n = 2 となります)。ws はオプション引数で、True に設定すると数列をワークシートのアクティブセル (現在選択されているセル) から右側に順次転記します (デフォルトでは False です)。一例として、n = 10 のコラッツ数列を並べてみます。
'[VBA] コラッツ数列(n=10) Sub Test_Collatz() Call Collatz(10, True) End Sub '実行結果: '10 5 16 8 4 2 1
コラッツ数列が 1 になるまでのステップ数を返すマクロも作っておきました。
'[VBA] コラッツ数列ステップ計算関数 Function Collatz_Step(n As Long) As Long Dim stp As Long If n < 2 Then n = 2 End If Do Until n < 2 stp = stp + 1 If n Mod 2 = 0 Then n = n / 2 Else n = 3 * n + 1 End If Loop Collatz_Step = stp End Function
たとえば、ワークシートの適当なセルに
=Collatz_Step(10)
と入力すると「6」が返ります。この関数を使って、横軸に正整数 n、縦軸に n が 1 に到達するまでのステップ数をプロットしてみると、以下のような結果が得られました。
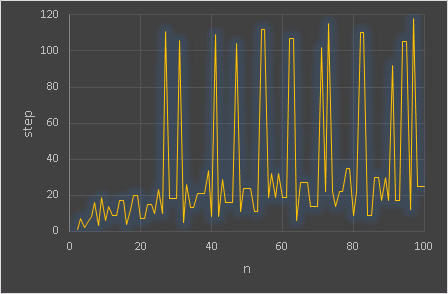
比較的短いステップで 1 に到達する数もあれば、長い手数を要する数もあります。このような直線グラフを見ても特に規則性がないように思えますが、散布図で描いてみると面白い図が現れます。
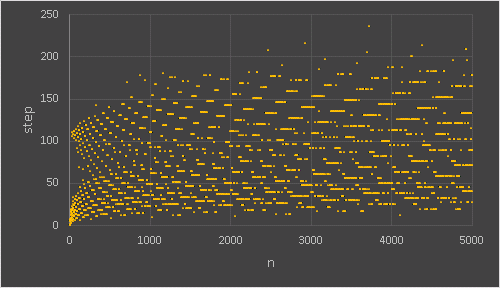
VBA の Long 型に格納できる値の上限は 2147483647 なので、コラッツ数列の中にこの値を超える項が出現するとオーバーフローとなってしまいます。オーバーフローを発生させる最小の初期値を発見するコードを載せておきます。
'[VBA] 任意の初期値を受け取ってコラッツ数列の最大値を返す関数
Function Collatz_Max(k As Long)
Dim n As Long
Dim max_val As Long
n = k
max_val = n
If n < 2 Then
n = 2
End If
Do Until n < 2
If n Mod 2 = 0 Then
n = n / 2
Else
n = 3 * n + 1
End If
If n > max_val Then
max_val = n
End If
Loop
Collatz_Max = max_val
End Function
'[VBA] オーバーフローが発生する数列の最小初期値を発見するマクロ
Sub Find_Overflow()
Dim i As Long, x As Long
On Error GoTo ErrLabel
For i = 5 To 300000
Collatz_Max(i)
Next i
ErrLabel:
Debug.Print i
End Sub
Find_Overflow() を実行すると 113383 が返ります。ですから、VBA で生成できるコラッツ数列の初期値は最大で 113382 ということになります。
【小説】VBAを駆使してコラッツ予想の意味を考えよう
【AI連載小説】数学のリズム、エクセルの旋律(35)
Excel VBAサークルのメンバー、真琴、研伸、月子は、ある日の勉強会で数学の謎めいた問題である「コラッツ予想」について話し合うことになりました。サークルの部屋では、Excelが開かれ、数学的なディスカッションが始まっていました。
真琴が疑問そうに言った。
「みんな、コラッツ予想って知ってるか?」
研伸が考え込みながら答えた。
「コラッツ予想って、自然数 n に対して次の操作を繰り返すと、最終的には必ず1に到達するという予想だよね?」
「その通り。具体的には、自然数が偶数なら2で割り、奇数なら3倍して1を足すという操作を繰り返すんだ」
そこに月子が話に加わる。
「それで、どうして最終的には必ず1にたどり着くんでしょう?」
真琴が考え深そうに説明する。
「これがなかなか解明されていないんだ。どんな自然数から始めても、この操作を繰り返すといずれは1になるというのがコラッツ予想」
「なるほど、それで実際にVBAを使って試してみるってのは面白そうだな」
真琴がExcelを起動する。
「そうだね。VBAで数列を生成して、この操作を適用してみると、数学的な予想がどう実現されているのか理解しやすくなるよ」
三人はコラッツ予想についてのディスカッションを深めながら、Excel VBAを駆使して数学的な謎に挑戦していくのでした。

エクセルや数学に関するコメントをお寄せください
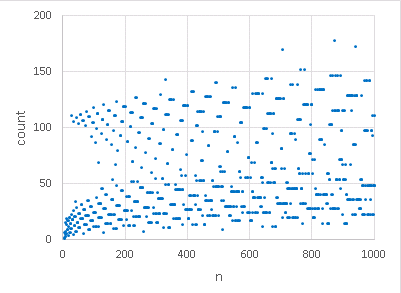
コラッツの予想が面白かったので、上記VBAを2~1000まで実行して
元数と手数の関係をグラフ化してみたら、不思議な図形になりました
3D円グラフ -> 宇宙の成り立ち
散布図 → バーンスレイのシダの親戚みたいな
ご参考までです
面白いですね!
貴重な情報、ありがとうございます!
さっそく、私も Excel でグラフを描いてみました。
コラッツ予想には、何か秘密が隠されているのかもしれませんね。
コメントありがとうございます。
このグラフの規則性だけでは説明できない不思議なドットの存在が興味深いです。
このサイトを楽しく拝見させていただいています。
最近VBAで考えているのが、EXCELの膨大な行数を時間経過にした、”世代”です。
何か不思議な世界があるかもしれません。
EXCELを使用したCOLLATZ予想の計算は、教育的には分かりやすい教材表現になりますが、注意すべきはEXCELの数値計算上の精度が低いことにあります。
整数の場合は、計算精度が15桁程度ですので、大きい数のCollatz数列は不正確になります。取り扱いできる最大の整数値を指定されると良いと思います。老爺心ながらコメントさせていただきます。
重要な御指摘、ありがとうございます。
確かに計算精度について明記しておく必要がありますね。
さっそく補足記事を書かせていただきました。
今後も何かお気づきの点がございましたら、ご指導のほどよろしくお願いいたします。