組合せと重複組合せの公式

組合せ

まずは 順列 の復習です。4 種類のアルファベット {a, b, c, d} から 3 つを取り出して 1 列に並べる方法は何通りあるか計算してみましょう。
 \[_4\mathrm{P}_3=4\times 3\times 2=24\,通り\]
そして、この中に含まれる順列は

[a, b, c],　[a, b, d],　[a, c, d],　[b, c, d]

のいずれかの文字セットで構成されています。各文字セットごとに整理分類して全部並べてみましょう。

abc,　acb,　bac,　bca,　cab,　cba
 
abd,　adb,　bad,　bda,　dab,　dba
 
acd,　adc,　cad,　cda,　dac,　dca
 
bcd,　bdc,　cbd,　cdb,　dbc,　dcb

ちゃんと 24 通りあります。そこで今度は使われている文字が同じものを区別しないで選び出す方法が何通りあるか考えます。つまり各行はまとめて 1 種類のものと考えて左端にある

abc,　abd,　acd,　bcd

だけを抜き出します。その総数は 24 ÷ 6 = 4 となります。各行にある順列の数は 3! と書くこともできるので、求める数 $x$ は
 \[x=\frac{_4\mathrm{P}_3}{3!}=\frac{24}{6}=4\]
と表すこともできます。

組合せ $_n\mathrm{C}_r$ の計算について１つ補足しておきます。たとえば、ある 10 個のものから 3 個を取り出すとき、取り出す 3 個を決めることは、あとに残る 7 個を決めているのと等しいことになります。つまり
 \[_{10}\mathrm{C}_3=_{10}\mathrm{C}_7=120\]
です。これは公式 (A) の $r$ を $n-r$ で置き換えても簡単に確かめることができます。すなわち
 \[_n\mathrm{C}_{n-r}=\frac{n!}{(n-r)!r!}=_n\mathrm{C}_r\]
となっています。

重複組合せ

この記事を書いているのは 6 月半ばです。そろそろアイスが食べたくなる季節ですね。さて、コンビニに行って、チョコアイス、バニラアイス、抹茶アイスの 3 種類から選んで 5 つを買うとしたら、その組合せは何通りあるでしょうか。ただしバニラを１つも買わないというような選択肢もありだとします。こうした問題を考えるときは「仕切り」を使うのが定石です。アイスを 〇 で表し、チョコ、バニラ、抹茶の間に適当に仕切りを入れてみましょう。
 

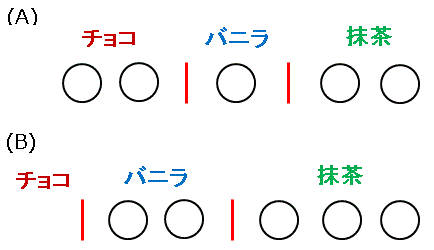
(A) はチョコ 2 個、バニラ 1 個、抹茶 1 個という状態を表しています。また、(B) は仕切りが一番左端にあり、これはチョコは１つも買わずに、バニラ 2 個、抹茶 3 個を選ぶという意味です。つまり 〇 と | を合わせた 7 個の順列を考えて、そこから 〇 と | の重複を取り除くことで選び方の総数を
 \[\frac{7!}{2!\:5!}=\frac{7!}{2!\,(7-2)!}={}_7\mathrm{C}_2=21\]
と計算することができます。これを一般化すると、$n$ 種類のものから重複を許して $r$ 個とることは、$r$ 個の 〇 と $n-1$ 個の | を 1 列に並べる順列に等しく、その選び方の総数は
 \[\frac{(r+n+1)!}{r!\,(n-1)!}=\:{}_{n+r-1}\mathrm{C}_r\]
と計算することができます。これを 重複組合せ (combination with repetition) とよび、$_n\mathrm{H}_r$ という記号で表します。