順列（円順列・同じものを含む順列・重複順列）

順列

　a, b, c, d, e という 5 つのアルファベットから 3 つの文字を選んで並べます。ただし文字を重複して選ぶことはしないものとします。その並べ方は何通りあるでしょう。

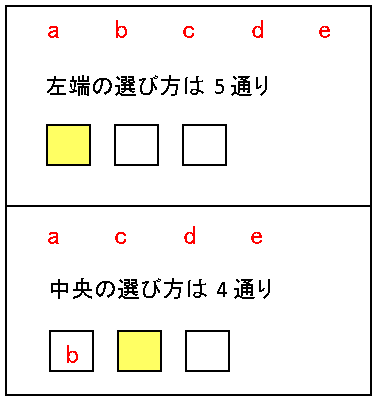
　図のように空白のマス目を使うとイメージしやすいです。
　まず 5 つの文字から 1 つを選んで左端に入れます。その方法は 5 通りですね。次に中央に入れる文字を選びます。1 度選んだ文字を再び使用することはできないので、4 文字から 1 つを選ぶことになります。つまり 4 通りです。同様に右端に入れる文字の選び方は 3 通りとなります。よって積の法則から、並べ方の総数は
　
\[5\times 4\times 3=60\]
となります。このとき、「abc, dae, ced」などの１つ１つを a, b, c, d, e から 3 個とった 順列 (permutation) とよびます。

　たとえば上の例では 5 個のものから 3 個をとるので、その総数は
　
\[_5\mathrm{P}_3=5\times 4\times 3=60\]
と書くことができます。また特に $n=r$ のときには
　
\[_n\mathrm{P}_n=n(n-1)(n-2)\:\cdots\:3\cdot 2\cdot 1=n!\]
で与えられます。$n!$ は 階乗 を表す記号です。通常は (A1) で計算する方法が簡単ですが、ある種の証明などでは順列の総数を階乗記号で表したほうが便利なこともあります。
　
\[\begin{align*}_n\mathrm{P}_r&=n(n-1)(n-2)\:\cdots\:(n-r+1)\\[6pt]&=\frac{n(n-1)(n-2)\:\cdots\:(n-r+1)(n-r)\:\cdots\:2\cdot 1}{(n-r)\:\cdots\:2\cdot 1}=\frac{n!}{(n-r)!}\end{align*}\]
　$0!=1$ と定義されているので、$n=r$ のときは $_n\mathrm{P}_n=n!$ となります。

円順列

　A, B, C, D の 4 人が丸いテーブルに座って食事をします。このとき、異なる順序の座り方は何通りあるのか数えてみましょう。
　
　

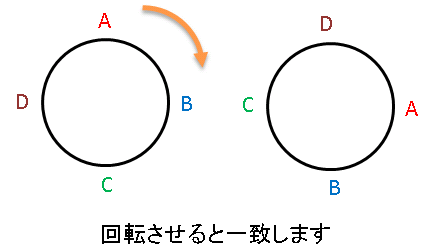
　上の図にあるように、回転して一致する場合は同じ並び方とします。
　そこで A さんを固定させて、残りの人の座り方を考えることにします。

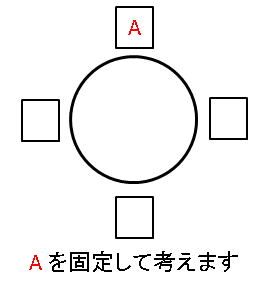
　その並び方の総数は $_3\mathrm{P}_3=3!=12$ 通りになります。

　このような順列のことを 円順列 (circular permutation) とよびます。

首飾り順列

　円順列とよく似たものに 首飾り順列 (necklace permutation) というものがあります。円順列と同じく平面内の回転操作に加えて、裏返すことによって一致するものは同じ並びとみなします。

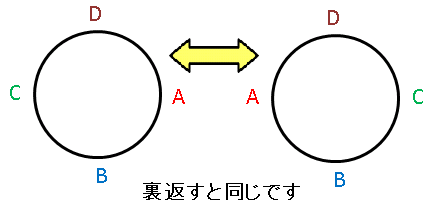
　各々の並び方に対して裏返しは 2 通りあるので、

　たとえば 6 個の異なる色の玉を用いて数珠をつくる方法は
　
\[\frac{(6-1)!}{2}=60\]
あります。

同じものを含む順列

　赤い玉 3 つと青い玉 2 つの並べ方の総数を調べてみましょう。考えやすいように、赤い玉には 1, 2, 3 という番号を、青い玉にも 1, 2 という番号を割り振ります。この 5 つの異なる玉の並び方は $5!$ 個あります。

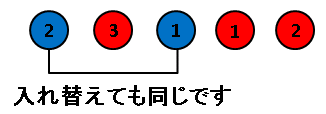
　そして番号によって区別しないことにすれば、上の図のように青い玉の 1 と 2 を入れ替えても同じ並び方ですし、赤い玉は 1, 2, 3 のどれを入れ替えても同じです。つまり並べ方の総数は
　
\[\frac{5!}{2!3!}=10\]
となります。

重複順列

　1, 2, 3, 4, 5 の 5 つの数字を用いてつくる 3 桁の整数はいくつあるのか考えてみます。ただし同じ数字を繰り返し使ってよいことにします。100 の位の選び方は 5 通り、10 の位も 5 通り、1 の位も 5 通りあるので、つくられる整数は全部で $5^3=125$ 個ということになります。

　このような順列を 重複順列 (permutations with repetition) とよびます。