区分求積法（Quadratures By Parts）

区分求積法と定積分

関数 $f(x)$ は区間 $[a,\ b]$ で連続であるとし、$f(x)$ と直線 $x=a,\ x=b$ および $x$ 軸によって囲まれる面積を $S$ とします。



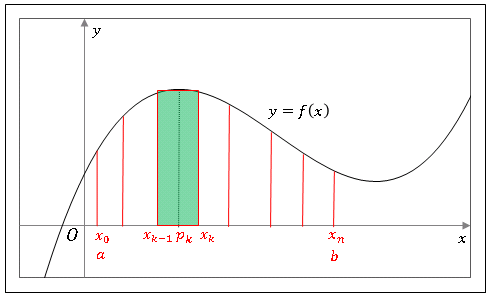
図のように区間 $[a,\ b]$ を $n+1$ 個の点
\[a=x_0,\ x_1,\ x_2,\ \cdots,\ x_{k-1},\ x_{k},\ \cdots,\ x_n=b\tag{1}\]
で分割して、それぞれの点から
\[f(x_0),\ f(x_1),\ f(x_2),\ \cdots,\ f(x_{k-1}),\ f(x_{k}),\ \cdots,\ f(x_n)\tag{2}\]
の各点に引いた垂線によって $S$ を帯状に分けます。さらに $x_{k-1}$ と $x_k$ の間に点 $p_k$ をとり、各々の帯の面積を底辺 $\Delta x_k=x_k-x_{k-1}$, 高さ $f(p_k)$ の長方形の面積で近似します。すべての長方形を足し合わせると
\[S_n=\sum_{k=1}^{n}f(p_k)\Delta x_k\tag{3}\]
と表されます。ここで分割数 $n$ を限りなく小さくすると、$\Delta x_k$ も限りなく小さくなります。このとき $S_n$ は $S$ に限りなく近づくので、その極限値
\[\lim_{n\rightarrow \infty}\sum_{k=1}^{n}f(p_k)\Delta x_k\tag{4}\]
を $f(x)$ の 定積分 (definite integral) と定義して、
\[\int_{a}^{b}f(x)dx=\lim_{n\rightarrow \infty}\sum_{k=1}^{n}f(p_k)\Delta x_k\tag{5}\]
のように表します。$a,\ b$ をそれぞれ積分下限、積分上限といいます。(5) は 不定積分 の記号 $\displaystyle \int dx$ とは全く別個に定義したものなので、現段階では不定積分との間の関連性は明らかではありません。

定積分の基本性質

定義 (5) より、定積分に関して次のような公式が成り立つことがわかります。
\[\begin{align*}\int_{a}^{b}\{f(x)+g(x)\}dx&=\int_{a}^{b}f(x)dx+\int_{a}^{b}g(x)dx\\[6pt]\int_{a}^{b}kf(x)dx&=k\int_{a}^{b}f(x)dx\end{align*}\tag{6}\]
両式を１つにまとめると、
\[\int_{a}^{b}\{kf(x)+lg(x)\}dx=k\int_{a}^{b}f(x)dx+l\int_{a}^{b}g(x)dx\tag{7}\]
と表せます。また、被積分関数が $f(x)=c$ ($c$ は定数) であるときには、
\[\int_{a}^{b}cdx=c(b-a)\tag{8}\]
となります。区間 $[a,\ b]$ で $f(x)\geq 0$ ならば
\[\int_{a}^{b}f(x)dx\geq 0\tag{9}\]
が成り立つことも明らかです。区間 $[a,\ b]$ で $f(x)\geq g(x)$ が成り立つなら、$f(x)-g(x)\geq 0$ なので、(9) より
\[\int_{a}^{b}\{f(x)-g(x)\}dx\geq 0\tag{10}\]
が成り立つので、
\[\int_{a}^{b}f(x)dx\geq\int_{a}^{b}g(x)dx\tag{11}\]
が成立します。また、積分の下限と上限が等しいとき、すなわち $b=a$ のとき、
\[\int_{a}^{a}f(x)dx=0\tag{12}\]
が成り立ちます。

平均値の定理

微分で表された平均値の定理においては、区間 $[a,\ b]$ において傾きが $f'(c)\ (a\lt c\lt b)$ となるような $c$ が必ず存在するとされていました。この記事では長方形 $f(c)(b-a)$ が定積分 $\displaystyle\int_{a}^{b}f(x)dx$ と等しくなるような $c$ が存在すると主張する、平均値の定理の積分形を導きます。



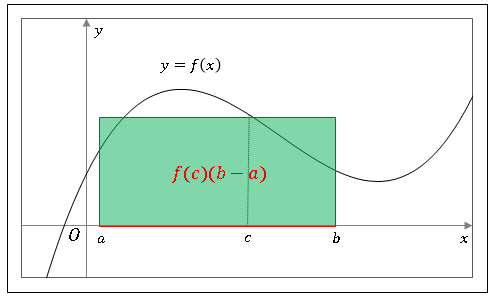
いま、$f(x)$ は区間 $[a,\ b]$ において連続で、区間内における最小値と最大値がそれぞれ $m,\ M$ であるとします。先ほど証明した定積分の性質
\[[a,\ b]\]
において
\[f(x)\geq g(x)\Longrightarrow\int_{a}^{b}f(x)dx\geq\int_{a}^{b}g(x)dx\]
を用いると、

\[\int_{a}^{b}mdx\leq \int_{a}^{b}f(x)dx \leq \int_{a}^{b}Mdx\tag{13}\]
という不等式が成り立ちます。すなわち
\[m(b-a)\leq \int_{a}^{b}f(x)dx \leq M(b-a)\tag{14}\]
各辺を $b-a$ で割ると
\[m\leq \frac{1}{b-a}\int_{a}^{b}f(x)dx \leq M\tag{15}\]
よって、$m\leq A\leq M$ を満たすある定数を $A$ として
\[\frac{1}{b-a}\int_{a}^{b}f(x)dx=A\tag{16}\]
となります。中間値の定理により、
\[f(c)=A\quad (a\lt c\lt)\tag{17}\]
となるような $c$ が必ず存在するので、
\[\frac{1}{b-a}\int_{a}^{b}f(x)dx=f(c)\tag{18}\]
を満たす $c$ が存在します。$c=a+s(b-a)$ とおくと
\[\int_{a}^{b}f(x)dx=(b-a)f(a+s(b-a))\quad (0\lt s\lt 1)\tag{19}\]
となり、これが積分で表された平均値の定理です。

微分積分学の基本定理

平均値の定理を使うと、不定積分と定積分の関係を明らかにすることができます。積分上限を変数 $x$ とする関数
\[F(x)=\int_{a}^{x}f(t)dt\tag{20}\]
を定義して、変数を $x$ から $\Delta x$ だけ動かしたときの定積分を計算すると
\[\begin{align*}F(x+\Delta x)&=\int_{a}^{x+\Delta x}f(x)dx\\[6pt]&=\int_{a}^{x}f(t)dt+\int_{a}^{x+\Delta x}f(t)dt\\[6pt]&=F(x)+\int_{a}^{x+\Delta x}f(t)dt\end{align*}\tag{21}\]
ここで先ほどの平均値の定理
\[\int_{a}^{b}f(x)dx=(b-a)f(a+s(b-a))\quad (0\lt s\lt 1)\]
を使うと、
\[\begin{align*}F(x+\Delta x)&=F(x)+(x+\Delta x-x)f(x+s\Delta x)\\[6pt]&=F(x)+\Delta x f(x+s\Delta x)\end{align*}\tag{22}\]
となるので、
\[\frac{F(x+\Delta x)-F(x)}{\Delta x}=f(x+s\Delta x)\tag{23}\]
ここで $\Delta x\rightarrow 0$ の極限をとると、
\[F'(x)=f(x)\tag{24}\]
が得られます。これは 微分積分学の基本定理 とよばれています。この定理を少し言い換えると
\[F(x)=\int_{a}^{x}f(t)dt\tag{25}\]
は $f(x)$ の原始関数のひとつです。いま、$F'(x)=f(x)$ を満たすような原始関数のひとつ $F_0(x)$ が見つかったとします。$F_0(x)$ に任意定数 $C$ を加えてもやはり原始関数なので、
\[\int_{a}^{x}f(t)dt=F_0(x)+C\tag{26}\]
$x=a$ とおくと左辺は $0$ になるので
\[0=F_0(a)+C\tag{27}\]
したがって、$C=F_0(a)$ と定まり、
\[\int_{a}^{x}f(t)dt=F_0(x)-F_0(a)\tag{28}\]
$x=b$ と置き直すと
\[\int_{a}^{b}f(t)dt=F_0(b)-F_0(a)\tag{29}\]
$F_0(x)$ は任意の原始関数なので $F(x)$ と置き直します。また、左辺の積分変数 $t$ も $x$ に置き換えると
\[\int_{a}^{b}f(x)dx=F(b)-F(a)\tag{30}\]
となります。すなわち、下限 $a$ から上限 $b$ の定積分は $F(b)$ から $F(a)$ を引いて得られることになります。積分下限と積分上限を入れ替えると、
\[\int_{a}^{b}f(x)dx=F(a)-F(b)\tag{31}\]
となるので、
\[\int_{b}^{a}f(x)dx=-\int_{a}^{b}f(x)dx\tag{32}\]
という公式も導かれます。

≫ Python高水準パッケージ SciPy による数値計算法