xsinxの積分・xcosxの積分

xsinxの積分

$x\sin x$ の積分公式です。導出することは難しくありませんが、できれば覚えてしまって、少しでも時間を節約したいところです：
 \[\int{x\sin{x}}dx=\sin{x}-x\cos{x}+C\tag{1}\]
【証明】$x \sin x$ の積分は部分積分によっても求められますが、$x\cos x$ を微分するほうがより簡単です：
 \[(x\cos{x})’ = \cos{x}-x\sin{x} = (\sin{x})’ – x\sin{x}\tag{2}\]
右辺に $x\sin{x}$ が現れています。この式を整理すると
 \[x\sin{x} = (\sin{x})’ – (x\cos{x})’\tag{3}\]
両辺を積分すると、
 \[\int{x\sin{x}}dx=\sin{x}-x\cos{x}+C\tag{4}\]
三角関数の変数が $mx$ になっているときは $t = mx$ と変換します：
 \[\begin{align*}\int x\sin{mx}dx&=\frac{1}{m^{2}}\int t\sin{t}\: dt\\&=\frac{1}{m^{2}}(\mathrm{sin}t-t\mathrm{cos}t)+C\\&=\frac{1}{m^{2}}\: \mathrm{sin}mx-\frac{x}{m}\mathrm{cos}mx+C\end{align*}\tag{5}\]
余力があれば、この $m$ を含んだ公式を覚えてしまいましょう。

【Excel】xsinxのグラフ

Excel で描いた $f(x)=x\sin x$ のグラフを載せておきます。
 
(≫ グラフデータの入った Workbook をダウンロード)
 

 
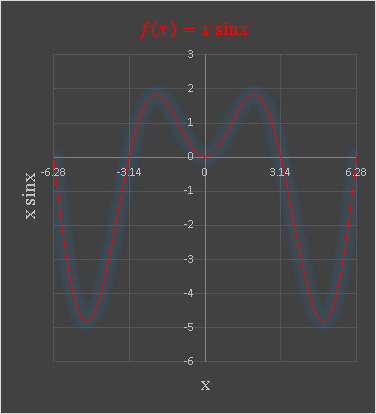
奇関数×奇関数なので、$x\sin x$ は偶関数です。
$x\sin x$ は定積分に特徴があります。公式 (1) より、
 \[\int_{0}^{\pi}x\sin xdx=\left[\sin x-x\cos x\right]^{\pi}_0=\pi\tag{6}\]
を得ます。これは曲線 $y=x\sin x$ と線分 $[0,\ \pi]$ で囲まれる領域の面積が円周率 $\pi$ (すなわち半径 $1$ の円の面積) に等しいことを意味します。

【VBA】xsinx の積分を計算するマクロ

$x\sin{x}$ を積分する VBA マクロを載せておきます。積分公式 (1) を使えば、以下のように簡単に実装できます。

'[VBA] xsinxの積分を返す関数
Function XSINX_INTEG(a As Double, b As Double)
    Dim val_a As Double, val_b As Double
    val_a = Sin(a) - a * Cos(a)
    val_b = Sin(b) - b * Cos(b)
    XSINX_INTEG = val_b - val_a
End Function

引数 a には積分の下端、引数 b には積分の上端を渡します。たとえば、ワークシートに「=XSINX_INTEG(0,PI())」と入力すると、円周率に近い値「3.141592654 …」が返ります。
 
シンプソンの公式を使って積分値を得るマクロは以下のようになります。

'xsinxの値を返すマクロ
Function XSINX(x)
    XSINX = x * Sin(x)
End Function

'シンプソンの公式でxsinxを数値積分するマクロ
Function XSINX_SIMPSON(a As Double, b As Double, n As Long)

    Dim h As Double, s As Double
    Dim k As Integer

    s = 0
    h = (b - a) / (2 * n)

    For k = 0 To n - 1
        s = s + XSINX(a + 2 * k * h) _
            + 4 * XSINX(a + (2 * k + 1) * h) _
            + XSINX(a + (2 * k + 2) * h)
    Next k

    XSINX_SIMPSON = s * h / 3

End Function

引数 a には積分の下端、引数 b には積分の上端を渡します。n は分割数で、大きな値を入れるほど精度が上がりますが処理時間も増えます。たとえば、ワークシートに「=XSINX_SIMPSON(0,PI(),100)」を入力すると、円周率に近い値「3.141592655 …」が返ります。

xcosxの積分

$x\cos{x}$ の不定積分公式です。
 \[\int{x\cos{x}}dx=\cos{x}+x\sin{x}+C\tag{7}\]
【証明】 $x\sin{x}$ を微分すると、
 \[x\sin{x}’ = \sin{x} + x\cos{x} = (-\cos{x})’ + x\cos{x}\tag{8}\]
となるので、式を整理すると、
 \[x\cos{x} = (\cos{x})’ + (x\sin{x})’\tag{9}\]
両辺を積分すると、$x\cos{x}$ の積分を得ます：
 \[\int{x\cos{x}}dx=\cos{x}+x\sin{x}+C\tag{10}\]
三角関数の変数が $mx$ になっているときは $t = mx$ と変換します：
 \[\begin{align*}\int x\mathrm{cos}mxdx&=\frac{1}{m^{2}}\int t\mathrm{cos}t\: dt\\&=\frac{1}{m^{2}}(\mathrm{cos}t+t\mathrm{sin}t)+C\\&=\frac{1}{m^{2}}\: \mathrm{cos}mx+\frac{x}{m}\mathrm{sin}mx+C\end{align*}\tag{11}\]

【Excel】xcosx のグラフ

下の図は Excel で描いた $f(x)=x\cos x$ のグラフです：
 

 
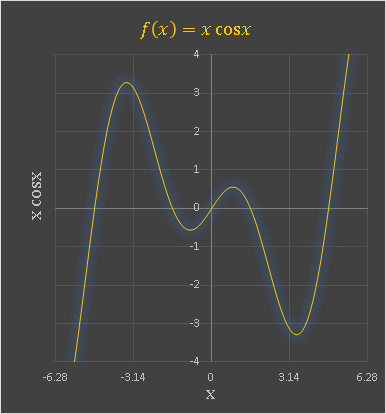
奇関数×偶関数なので、$x\cos x$ は奇関数です。

【VBA】xcosxの積分を計算するマクロ

公式 (10) を使って $x\cos{x}$ の積分を計算するマクロを載せておきます。

'xcosxの定積分の値を返すユーザー定義関数
Function XCOSX_INTEG(a As Double, b As Double)
    Dim val_a As Double, val_b As Double
    val_a = Sin(a) - a * Cos(a)
    val_b = Sin(b) - b * Cos(b)
    XCOSX_INTEG = val_b - val_a
End Function

たとえば、ワークシートの適当なセルに「=XCOSX_INTEG(0,2*PI())」を入力すると「-6.283185307」が返ります。

x^2 sinxの積分・x^2cosx の積分

公式を使って、$x^2\sin{x}$ の積分を求めることができます。$x^2\cos{x}$ を微分すると
 \[(x^2\cos{x})^{\prime}=2x\cos{x}-x^2\sin{x}\tag{12}\]
となって、右辺に $x^2\sin{x}$ の項が現れます。移項して整理すると
 \[x^2\sin{x}=2\cos{x}dx-(x^2\cos{x})^{\prime}\tag{13}\]
両辺を積分すると
 \[\int{x^2\sin{x}}dx=\int{2\cos{x}}dx-x^2\cos{x}\tag{14}\]
ここで公式 (10) を使って右辺第 1 項の積分を実行すると、
 \[\int{x^2\sin{x}}dx=2(x\sin{x}+\cos{x})-x^2\cos{x}+C\tag{15}\]
を得ます。整理すると
 \[\int{x^2\sin{x}}dx=(2-x^2)\cos{x}+2x\sin{x}+C\tag{16}\]
となります。同様に $x^2\sin{x}$ を微分して公式 (1) を使うと、
 \[\int{x^2\cos{x}}dx=(x^2-2)\sin{x}+2x\cos{x}+C\tag{17}\]
が得られます。

f(x)sinxの積分・f(x)cosxの積分

次の公式は無理に覚える必要はありませんが、どこかに控えておくと、証明に役立つことがあります。$f^{n}(x)$ は $n$ 階導関数を表す記号です。
 \[\int f(x)\mathrm{sin}xdx=\sum_{k=0}^{\infty }(-1)^k\: [f^{(2k+1)}(x)\mathrm{sin}x-f^{(2k)}(x)\mathrm{cos}x] \tag{18}\]
積分定数 $C$ は省略してあります。

【証明】単純に部分積分を実行します。
 \[\begin{align*}I(x)=\int f(x)\mathrm{sin}xdx&=-f(x)\mathrm{cos}x+\int f^{(1)}(x) \mathrm{cos}xdx\\&=-f(x)\mathrm{cos}x+f^{(1)}(x) \mathrm{sin}x-\int f^{(2)}(x) \mathrm{sin}xdx\end{align*}\tag{19}\]
最後の積分は $I(x)$ の $f(x)$ のところを $f”(x)$ に置き換えただけなので、あとは繰り返しになります。
 \[\begin{align*}I(x)=&-f(x)\mathrm{cos}x+f^{(1)}(x)sinx\\&-\left \{ -f^{(2)}(x) \mathrm{cos}x+f^{(3)}(x) \mathrm{sin}x-\int f^{(4)}(x) \mathrm{sin}xdx \right \}\\&=[f^{(1)}(x)-f^{(3)}(x)+f^{(5)}(x)+\cdots]\: \mathrm{sin}x\\&+[-f^{(0)}(x)+f^{(2)}(x)-f^{(4)}(x)+\cdots]\: \mathrm{cos}x\\&=\sum_{k=0}^{\infty }[(-1)^kf^{(2k+1)}(x)\mathrm{sin}x+(-1)^{k+1}f^{(2k)}(x)\mathrm{cos}x]\\&=\sum_{k=0}^{\infty }(-1)^k\: [f^{(2k+1)}(x)\mathrm{sin}x-f^{(2k)}(x)\mathrm{cos}x]\end{align*}\tag{20}\]
和は $n$ 階導関数 $f^n (x)$ が $0$ になるまでとればよいので、$f(x)$ が三角関数のように微分に対して循環しない限りは有限項の級数となります。ですから実用的に考えると、
 \[\int f(x)\mathrm{sin}xdx=[f^{(1)}(x)-f^{(3)}(x)]\, \mathrm{sin}x+[f^{(2)}(x)-f^{(0)}(x)]\, \mathrm{cos}x \tag{21}\]
ぐらいまでを覚えておけば充分です。$f(x) = x,\:f(x) = x^2$ について直ちに次の公式が得られます。
 \[\begin{align*}&\int x\mathrm{sin}xdx=-x\mathrm{cos}x-\mathrm{sin}x+C\\&\int x^2\mathrm{sin}xdx=(2-x^2)\, \mathrm{cos}x+2x\, \mathrm{sin}x+C\end{align*}\tag{22}\]　
同じようにして、
 \[\int f(x)\mathrm{cos}xdx=\sum_{k=0}^{\infty }(-1)^k\: [f^{(2k)}(x)\mathrm{sin}x+f^{(2k+1)}(x)\mathrm{cos}x]\tag{23}\]
という公式も得られます。$f^{(3)} (x)$ までの導関数を使って簡略的に書くと
 \[\int f(x)\mathrm{cos}xdx=[f^{(0)}(x)-f^{(2)}(x)]\, \mathrm{sin}x+[f^{(1)}(x)-f^{(3)}(x)]\, \mathrm{cos}x \tag{24}\]
となります。たとえば、$f(x) = x,\:f(x) = x^2$ とすると
 \[\begin{align*}&\int x\mathrm{cos}xdx=x\mathrm{sin}x+\mathrm{cos}x+C\\&\int x^2\mathrm{cos}xdx=(x^2-2)\, \mathrm{sin}x+2x\, \mathrm{cos}x+C\end{align*}\tag{25}\]
という公式を得ます。