連続と不連続
下図のように、関数 $f(x)$ が定義された区間内に 1 点 $a$ をとります。
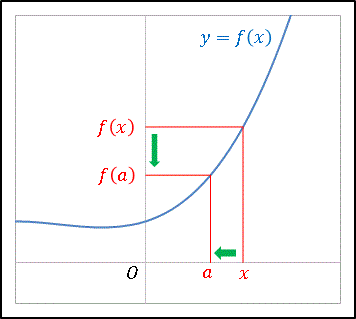
$x$ を限りなく $a$ に近づけたとき、つまり、$|x-a|\rightarrow 0$ で、
\[|f(x)-f(a)|\rightarrow 0\]
となるのであれば、関数 $f(x)$ は $x=a$ で連続(coutinuous)であるといいます。極限記号を使って書くと
\[\lim_{x \rightarrow a}|f(x)-f(a)|=0\]
すなわち
\[\lim_{x \rightarrow a}f(x)=f(a)\]
であれば関数 $f(x)$ は $x=a$ で連続です。
① $f(x)$ が $a$ の前後で定義されている。
② $\displaystyle \lim_{x\rightarrow a}f(x)$ が存在している。
③ $\displaystyle \lim_{x\rightarrow a}f(x)=f(a)$
もし区間内の任意の点 $a$ で上の条件が成り立つのであれば、 $y=f(x)$ はその区間内で連続であるといいます。直感的に説明すると、関数のグラフを鉛筆でなぞったときに一度も紙面から鉛筆の先が離れなければ、その関数は区間内で連続だということです。しかしこの定義だけでは「区間の端ではどうなるのか?」という疑問が生じます。たとえば下図のように区間 $[\alpha,\:\beta]$ で定義された関数 $f(x)$ があるとします。
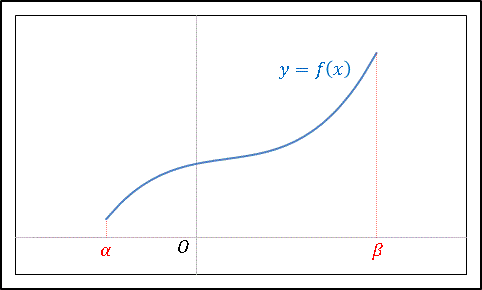
この場合、$x$ を負の方向(左側)から $\alpha$ に近づけることができません。しかし $x$ を正方向(右側)から $\alpha$ に近づけたときの極限値 $\displaystyle \lim_{x\rightarrow \alpha+0}f(x)$ が存在し、 $\displaystyle \lim_{x\rightarrow \alpha+0}f(x)=f(\alpha)$ であるならば、関数 $y=f(x)$ は $x=\alpha$ で連続であると考えます。同様に端点 $\beta$ においても、 $\displaystyle \lim_{x\rightarrow \beta-0}f(x)=f(\beta)$ ならば、関数 $y=f(x)$ は $x=\beta$ で連続です。
$f(x)=\log x$ は $x=1$ で連続です。なぜなら $x=1$ の前後で $f(x)=\log x$ は定義され、$\displaystyle \lim_{x\rightarrow 1}f(x)$ が存在し、$\displaystyle \lim_{x\rightarrow 1}f(x)=\log 1=0$ となるからです。同様に $x \gt 0$ のあらゆる点で連続であることがわかります。
連続条件を1つでも満たさない場合、関数 $y=f(x)$ は点 $x=a$ において不連続 (discontinuous)であるといいます。たとえば $y=1/(x-1)$ は $x=1$ で不連続です。
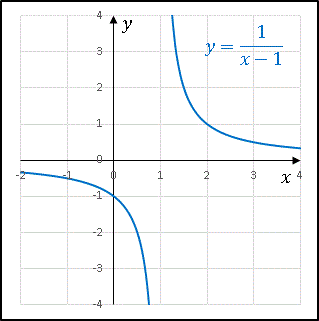
そもそも $f(1)$ が定義されていないし、 $\displaystyle \lim_{x\rightarrow 1}f(x)$ も存在しないからです。
以下に連続関数の性質をまとめておきます。
\[kf(x),\quad f(x) \pm g(x),\quad f(x)g(x)\]も連続であり、$g(x) \neq 0$ の点について
\[\frac{f(x)}{g(x)}\]もまた連続である。
この性質から多項式
\[f(x)=a_0x^n+a_1x^{n-1}+\:\cdots\: a_n\]
は全て連続であることがわかります。また 2 つの多項式 $f(x),\:g(x)$ があって、それぞれを分子分母とする関数 $y=f(x)/g(x)$ , すなわち有理関数もまた分母が 0 になる点を除けば連続です。
合成関数 $g(f(x))$ は $x=a$ で連続となる。
すなわち $\cos (\cos x)$ や $\exp (x^3)$ などは実数全域で連続です。
いたるところで滑らかな関数は連続です。言い換えると「微分可能な関数は連続です」。
【微分可能な関数は連続であることの証明】
ある区間で関数 $y=f(x)$ が定義されていて微分可能であるならば、
\[\lim_{x\rightarrow 0}\frac{\Delta y}{\Delta x}=\frac{dy}{dx}\]
が存在します。つまり
\[\lim_{x\rightarrow 0}\Delta y=\frac{dy}{dx}\lim_{x\rightarrow 0}\Delta x=0\]
となるので、$y=f(x)$ はこの区間で連続です。
しかし連続であるからといって、その関数が微分可能であるとはいえません。たとえば原点で折れ曲がる $f(x)=|x|$ という関数について考えてみます。この関数は $x=0$ でも確かに連続ではありますが、
\[\Delta y=f(0+\Delta x)-f(0)=|\Delta x|\]
となるので、$\Delta x \gt 0$ では
\[\frac{\Delta y}{\Delta x}=\frac{\Delta x}{\Delta x}=1\]
であり、$\Delta x \lt 0$ では
\[\frac{\Delta y}{\Delta x}=\frac{-\Delta x}{\Delta x}=-1\]
となってしまって微分は不可能です。
C^n級関数 (滑らかさの度合い)
関数 $f(x)$ が連続であるとき「関数 $f(x)$ は $C^0$ 級に属している」といいます。また $f(x)$ が 1 回微分可能で、その導関数 $f'(x)$ が連続であることを「$C^1$ 級に属している」といいます。この定義からわかるように、$C^1$ 級に属している関数は同時に $C^0$ 級にも属しています。一般に関数 $f(x)$ が $n$ 回連続微分可能で、$f^{(n)}(x)$ が連続であるならば、その関数は「$C^{n}$ 級に属している」といいます。たとえば $y=|x|$ は連続なので $C^0$ 級に属していますが、$x=0$ で $f'(x)$ が定義されないので $C^1$ 級には属していません。次の関数は連続なので $C^0$ 級に属しています。
\[f(x)=\left\{\begin{matrix}x^2\quad &(x\geq 0)\\[6pt]-x^2\quad &(0\lt x)\end{matrix}\right.\]
この関数を微分してみると
\[f'(x)=\left\{\begin{matrix}2x \quad &(x\geq 0)\\[6pt]-2x\quad &(0\lt x)\end{matrix}\right.\]
となって、やはり連続なので $C^1$ 級にも属しています。しかし $x=0$ で $f^{\prime\prime}(x)$ が定義されないので $C^2$ 級には属していません。普段扱っているような初等関数のほとんどは何度でも微分可能であり、そのような関数は「$C^{\infty}$ 級に属している」といいます。たとえば 2 次関数 $f(x)=x^2$ は
\[f'(x)=2x,\quad f^{\prime\prime}(x)=2,\quad f^{\prime\prime\prime}(x)=0,\quad f^{(4)}(x)=0,\cdots\]
というように無限回の微分が可能なので $C^{\infty}$ 級に属しています。同じように $\sin x$ や $\cos x$ もまた $C^{\infty}$ 級に属しています。

エクセルや数学に関するコメントをお寄せください