(1+i)z+a+i=0の解が複素平面上に描く軌跡

【CX01】複素数係数一次方程式の解が描く軌跡

複素数 $z$ に関する一次方程式
\[(1+i)z+a+i=0\]の解は複素数平面上でどのような軌跡を描きますか。$a$ は実数パラメータとします。
 
【ヒント】まずは $z$ の係数を外すことを考えます。

【解答】$z$ の係数を有理化するのが定石です：
 \[(1+i)z+a+i=0\]
の両辺に $1-i$ をかけると
 \[2z+(a+i)(1１-i)=0\]\[2z+a+1+i(1-a)=0\]\[z=\frac{1}{2}[-a-1+(a-1)i]\]
実部を $x$, 虚部を $y$ とおくと、
 \[x=-\frac{1}{2}(a+1),\quad y=\frac{1}{2}(a-1)\]
両式からパラメータ $a$ を消去すると、解の軌跡として
 \[y=-x-1\]
が得られます。すなわち複素数平面上の点は
 \[z=x+iy=x-i(x+1)\]
で表されることになります。
 

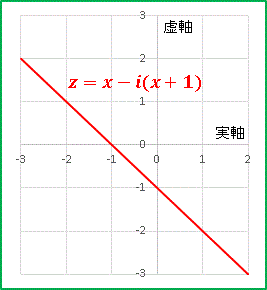
【補足】実数 $x$ について、
 \[f(a)x+g(a)=0\]
という一次方程式を考えたときに、解は $f(a),\:g(a)$ の形によらず、
 \[x=-g(a)/f(a)\]
となって複素数平面の実軸上を動くだけです（ただし、その動き方は $f,\:g$ の形によって多様です）。これを
 \[f(a)z+g(a)=0\]
のように、変数と係数を複素数に変えると世界が平面上に広がります。$f$ や $g$ の形によってはより複雑な軌跡を描くことになり、一気に問題は複雑化して媒介変数関数の微積分が必要となります（場合によっては数値計算でないと解けないこともあります）。そうした問題については、もう少し先で扱ってみることにしますので、楽しみに待っていてください。　

【CX02】iのn乗を計算します

複素数の極形式 $z=re^{i\theta}$ を用いて $i^n$ を計算してください。ただし $n$ は $0$ 以上の整数とします。
 
【ヒント】周期性があるので $n$ についての場合分けが必要です。

【解答】$i$ を極形式で表すと $i=e^{i\frac{\pi}{2}}$ なので、
 \[\large i^n=e^{i\frac{n\pi}{2}}\]
となります。$n=0,\:1,\:2,\:3,\:4$ で計算してみると、
 \[\begin{align*}&i^0=e^0=1\\[6pt]&i^1=e^{i\frac{\pi}{2}}=\cos\frac{\pi}{2}+i\sin\frac{\pi}{2}=i\\[6pt]&i^2=e^{i\pi}=\cos\pi+i\sin\pi=-1\\[6pt]&i^3=e^{i\frac{3\pi}{2}}=\cos\frac{3\pi}{2}+i\sin\frac{3\pi}{2}=-i\\[6pt]&i^4=e^{i2\pi}=\cos 2\pi+i\sin 2\pi=-1\end{align*}\]
周期性から $n=0$ と $n=4$ は同じ値をとります。
したがって、$i^n$ は $k$ を $0$ 以上の整数として
 
① $n=4 k$ のとき $1$
② $n=4 k+1$ のとき $i$
③ $n=4 k+2$ のとき $-1$
④ $n=4 k+3$ のとき $-i$
 
となります。とくに $n=2$ のとき
 \[i^2=-1\]
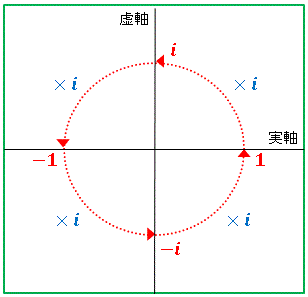
という虚数の有名な性質が現れています。このように、$i$ を掛けるという演算は複素平面上における回転操作を表しています。
 

【補足】極形式を使えば $\sqrt{i}$ の計算も簡単です。
 \[\large i^n=e^{\frac{n\pi}{2}}\]
において $n=1/2$ とおけば、
 \[\large i^n=e^{\frac{\pi}{4}}=\frac{\sqrt{2}}{2}(1+i)\]
という値が得られますが、これは複素数平面上で実数 $1$ を正方向（反時計回り）に $45^\circ$ 回転させる操作に対応します。 $i$ を基準にすると負の方向（時計回りに）$45^\circ$ の回転ですから、これは「平方根をとる」というイメージに合いますね。

【CX03】三角級数の公式の証明

オイラーの公式 $e^{i\theta}=\cos\theta+i\sin\theta$　を用いて三角級数の公式
 \[\begin{align*}\sum_{k=0}^{n}\cos k\theta=\frac{\sin[(n+1)\theta /2\:]}{\sin(\theta/2)}\:\cos\:\frac{n\theta}{2}\\\sum_{k=0}^{n}\sin k\theta=\frac{\sin[(n+1)\theta/2\:]}{\sin(\theta /2)}\:\sin\:\frac{n\theta }{2}\end{align*}\]
を証明してください。

【解答】極形式 $e^{i\theta}$ の形から等比級数の和を求めておけば、最後に実部と虚部をとると $\cos k\theta$ と $\sin k\theta$ の和をまとめて求めることができます。
 \[S=1+e^{i\theta}+e^{i2\theta}+\cdots\]
とおけば、初項 $1$、公比 $e^{i\theta}$, 項数 $n+1$ の等比数列の和ですから、
 \[S=\frac{1-(e^{i\theta })^{n+1}}{1-e^{i\theta }}\]
と求めることができます。問題はここからで、分母と分子をうまく変形していかなくてはなりません。そのためによく知られた公式
 \[\sin\theta=\frac{e^{i\theta}-e^{-i\theta}}{2i}\]
を用います。
 \[\begin{align*}&1=e^{-i\frac{\theta}{2}}e^{i\frac{\theta}{2}}\\[6pt]
&e^{i\theta}=e^{i\frac{\theta}{2}}e^{i\frac{\theta}{2}}\end{align*}\]
のように変形すると分母は
 \[e^{i\frac{\theta}{2}}(e^{-i\frac{\theta}{2}}-e^{i\frac{\theta}{2}})=-2ie^{i\theta}\sin\frac{\theta}{2}\]
となり、また分子は
 \[-2ie^{i(n+1)\theta}\sin\frac{(n+1)\theta}{2}\]
となるので、
 \[S=\frac{\sin[(n+1)\theta /2]}{\sin[\theta /2]}\large{e^{\frac{in\theta}{2}}}\]
となります。実部と虚部をとって
 \[\begin{align*}I=\mathrm{Re}S=\sum_{k=0}^{n}cosk\theta=\frac{\sin[(n+1)\theta /2\:]}{\sin(\theta/2)}\:\cos\:\frac{n\theta}{2}\\J=\mathrm{Im}S=\sum_{k=0}^{n}\sin k\theta=\frac{\sin[(n+1)\theta/2\:]}{\sin(\theta/2)}\:\sin\:\frac{n\theta }{2}\end{align*}\]
という三角級数の公式を得ます。

【CX04】複素数係数二次方程式

(1) 複素数定数 $a,\;b,\;c$ を係数とする二次方程式
\[az^2+bz+c=0\quad (a\neq 0)\]の解を求めてください。
(2) $z^2+(1+i)z+3i=0$ の解を求めてください。
 
【ヒント】(1) 実数における二次方程式の解の公式と同じように導出しますが、符号の記述が少しだけ異なります。
　【解答】(1) 与式を平方完成して解の公式を得ます：
 \[\begin{align*}&az^{2}+bz+c=0\\&a\left(z+\frac{b}{2a}\right)^{2}+c-\frac{b^{2}}{4a^{2}}=0\\&z=\frac{-b+\left(b^{2}-4ac\right)^{1/2}}{2a}\end{align*}\]
実数係数のときの公式とは違って $(\:)^{1/2}$ の前に ± がついていませんが、$()^{1/2}$、すなわち 2 乗根が 2 つの解を表しているからです。それは () の中身が実数であっても同じです。たとえば 1 の 2 乗根は

11/2 = exp[i(k + 1)π] = 1, －1

となってきちんと正負の解が現れるようになっています。

(2) 解の公式に a = 1, b = 1 + i, c = 3i を代入して
　
\[z=\frac{1}{2}\left [ -1-i+(-10i)^{1/2} \right ]\]
　ここで、
　
\[\begin{align*}
-i&=exp\left [ i\left ( -\frac{\pi }{2}+2k\pi \right ) \right ]\\
(-i)^{1/2}&=exp\left [ i\left ( -\frac{\pi }{4}+k\pi \right ) \right ]\end{align*}\]
となるので、

\[\begin{align*}z_{1}&=\frac{1}{2}\left [ -1+\sqrt{5}-(1+\sqrt{5})i \right ]\\
z_{2}&=\frac{1}{2}\left [ -1-\sqrt{5}-(1-\sqrt{5})i \right ]\end{align*}\]
という解が得られます。