変動係数 (Coefficient of variation)
$n$ 個のデータ $x_1,\:x_2,\:\cdots,\:x_N$ があったとき、標準偏差 $\sigma$ は
\[\sigma=\sqrt{V}=\sqrt{\frac{\sum_{i=1}^{N}(x_i-m)^2}{n}}\]
で与えられます。ここで $V$ は分散、$m$ は平均です。標準偏差はデータのばらつき具合を表しますが、平均値や単位の異なるデータ同士で標準偏差を比較しても意味はありません（式の中に平均値からの差分が含まれているので、平均値の大きなデータの標準偏差は大きくなります）。
たとえば、ある集団の身長の標準偏差が 12 cm, 体重の標準偏差が 9 kg だったとしても、身長のほうが体重よりばらつきが多いとは言えないのです。そこで標準偏差を平均で割って無次元の量を定義します。
\[CV=\frac{\sigma}{m}\]
この量を 変動係数 (Coefficient of variation) とよび、異なる平均値や単位をもつデータ同士のばらつきを比較するために用いられます。たとえば
平均身長 170 cm 標準偏差 12 cm
平均体重 60 kg 標準偏差 9 kg
というデータがあった場合、変動係数はそれぞれ
身長の変動係数 $=12/170=0.07$
体重の変動係数 $=9/60=0.15$
となるので、体重のほうがばらつきが大きいことになります。
Excel で変動係数を計算する
Excel 関数を使って 変動係数 を計算してみましょう。あるクラスから無作為に 10 名を選んで身長と体重のデータを記録すると次のようになったとします。
| 番号 | 身長 [cm] | 体重 [kg] |
|---|---|---|
| 1 | 161.24 | 59.99 |
| 2 | 162.67 | 61.48 |
| 3 | 157.99 | 55.86 |
| 4 | 172.04 | 64.74 |
| 5 | 169.97 | 61.02 |
| 6 | 168.4 | 59.47 |
| 7 | 179.52 | 83.33 |
| 8 | 152.22 | 55.85 |
| 9 | 166.18 | 59.7 |
| 10 | 153.19 | 58.19 |
Excel で分母が $n$ の標準偏差（母集団標準偏差）を計算する関数は
です。Excel2007 以前のバージョンでは STDEVP関数を使用してください。一般には引数に範囲を指定して使用します。平均値は AVERAGE関数で計算できるので、D14 セルには
と入力すると身長の変動係数 0.0496 が得られます。
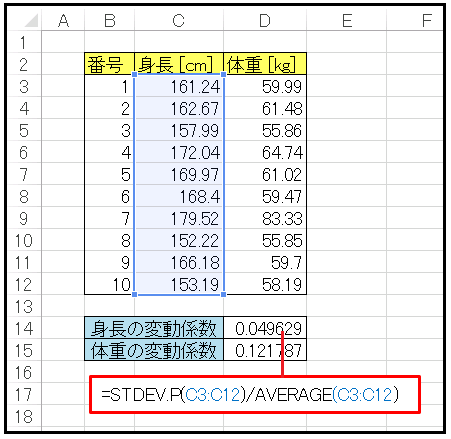
同様に D15 セルには
と入力して 0.1218 を得るので、体重のほうがばらつきが大きいことがわかります。
次のように VBA の標準モジュールに 変動係数 の値を返す関数を用意しておけば、変動係数の定義式を忘れても簡単に呼び出すことができます。
Function CV(x As Range)
CV = WorksheetFunction.StDev_P(x) / WorksheetFunction.Average(x)
End Function
上のコードを標準モジュールに貼り付けて、適当なセルに
と入力すれば、先ほどと同じ結果 0.0496 が得られます。
