【Excel】ゴールシークによる非線形方程式の求解

ゴールシーク

Excel には「入力した数式がある値に等しくなるような数値」を探すゴールシーク機能が備えられています。この機能を使うと難しい非線形方程式の数値解を簡単に求めることができます。

ゴールシークによる2次方程式の求解

最初に簡単な例として $x^2-1=0$ を ゴールシーク を使って解いてみます。下図にあるように、セルB2 に

=B4^2-1

と入力しておきます。


現段階ではセルB4 は空白なので、B4 には 0 の値が代入されて -1 という値が表示されています。次に [データ]をクリックします（下図）。


表示されるメニューから [What-If分析]、[ゴールシーク] の順に選択します（下図）。


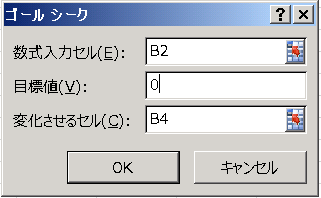
[ゴールシーク] のダイアログボックスが現れるので、[数式入力セル] に B2、[目標値] に 0、[変化させるセル] に B4 を入力して [OK] を押します。


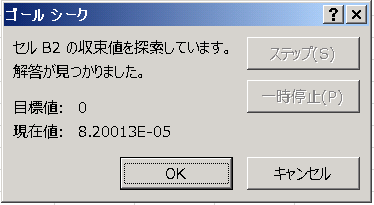
しばらく待つと、計算を終了して次のような画面が表示されます。


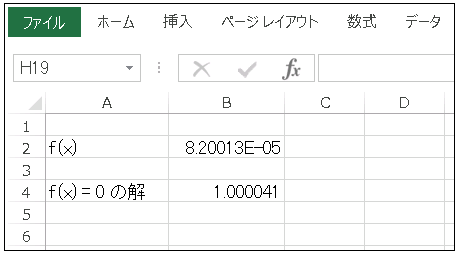
収束の目標値は 0 ですが、数値解法なので実際の収束値は僅かに誤差があります。セルB4 には方程式の解が表示されますが、収束値のずれに伴って、こちらも実際の解 $x=1$ から若干ずれます（下図）。


得られたのは正の解ですが、下図のようにゴールシークを実行する前にセルB4 に予め負の値を入れておくと、$x=-1$ に対応する解を得ることができます。

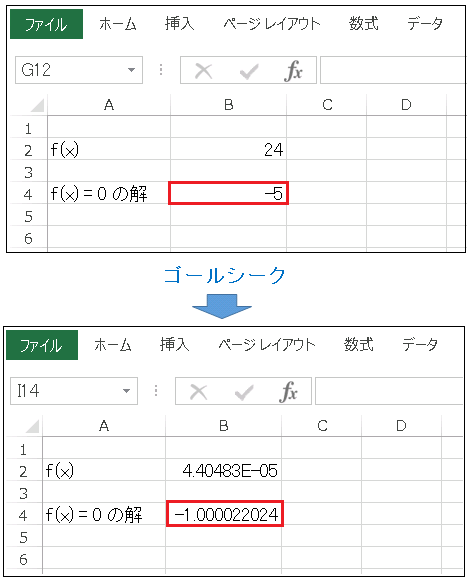
ゴールシークによる非線形方程式の求解

このような挙動から、内部では ニュートン・ラフソン法 のようなアルゴリズムを使っていることが推測できます。したがって、ゴールシークで方程式 $f(x)=g(x)$ を解く場合、予め Excel のグラフ機能を使って関数 f(x) と g(x) を重ねてプロットするなどして、交点の数とおおよその解のある場所を下調べしておく必要があります。例として方程式
\[\cos(x)+x\log(x)=2\]
を解いてみましょう。最初に $f(x)=\cos(x)+x\log(x)$ と $g(x)=2$ をグラフにプロットして概観を把握します（下図参照）。


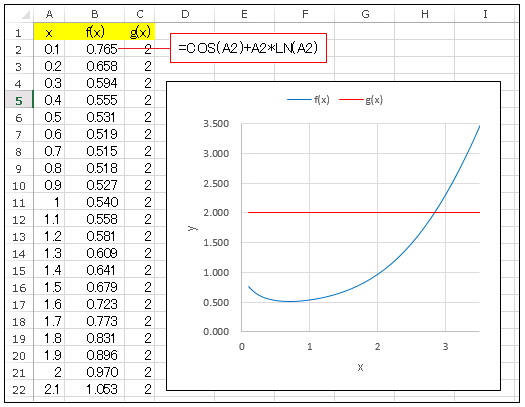
交点の数は 1 個なので、この方程式の解は 1 個であることがわかります。また、その解は $x=3$ 付近にあることもわかります。セルB2 には

=COS(B4)+B4*LN(B4)

と入力しておきます。セルB4 が空白のままだと LN関数の引数に 0 が渡されてエラーになる（$\log 0$ は定義されない）ので、セルB4 には予め 3 を入れておきます（下図）。正数であればどのような値を入れておいても構わないのですが、二分法やニュートン・ラフソン法では、初期値と解析解が近いほど計算が速くなります。


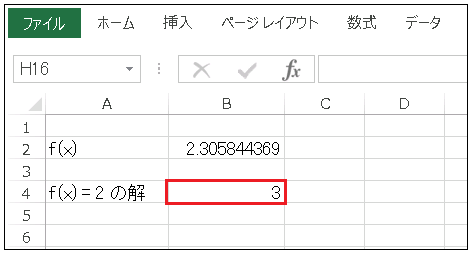
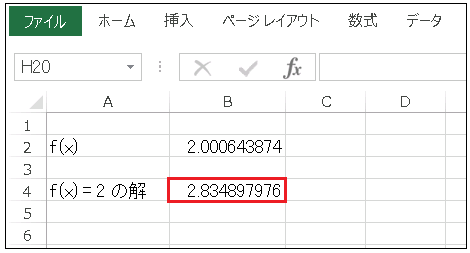
先ほどと同様の手順（ただし [目標値] は 2 に設定しておきます）でゴールシークすると、下図のように $x=2.835$ という解が得られます。