各位の数字がすべて異なる 3 桁の奇数

【PS01】各位の数字がすべて異なる三桁の奇数を数えます

各位の数字がすべて異なる 3 けたの奇数はいくつありますか？

【ヒント】確率統計分野の第 1 問は数え上げの基本問題です。百位、十位、一位それぞれに何通りの数が入るかを考えます。
　
【解答】一位が奇数であることは決まっていますから、$1,\;3,\;5,\;7,\;9$ の $5$ 通り。十位には $0$ を選べますが、百位には $0$ を選べないので、一位のそれぞれの場合に対して十位のとりうる場合を数えてしまうと、十位に $0$ を選んだ場合と選ばなかった場合で百位のとりうる場合の数が異なってしまいます。そこで一位の $5$ 通りに対して、百位のとりうる数をかぞえると、$9$ 通りから一位で選んだ数を除いて $8$ 通り。十位は $0$ から $9$ の $10$ 通りから一位と百位で選んだ数を除いて $8$ 通り。よって全部で
\[5\times 8\times 8=320\;通り\]
となります。

【PS02】長さの異なる棒を選んで三角形をつくります

長さが 1cm, 3cm, 5cm, 7cm, 9cm の 5 本の棒があります。このうちの 3 本を取り出して三角形をつくると、何種類のちがったものができますか。

【ヒント】選んだ棒の種類によって三角形ができる場合とできない場合があるので、条件に合う組合せを数え上げます。
　
【解答】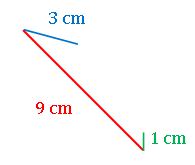本問で条件反射的に「 $5$ 個の中から $3$ 個を選ぶから ${}_{5}\mathrm{C}_{3}=10$ 通り！」などと解答してしまうと大変です。たとえば図にあるように、$9\,\mathrm{cm},\;3\,\mathrm{cm},\;1\,\mathrm{cm}$ の棒を選んでも三角形をつくることはできません。つまり選んだ棒の長さを $a\gt b\gt c$ とすれば、三角形の成立条件
\[a\lt b+c\]
を満たしていなければなりません。そのような組み合わせは
\[(9,\:7,\:5),\;(9,\:7,\:3),\;(7,\:5,\:3)\]
の $3$ 種類だけです。