完全微分型方程式
次のような微分方程式を考えてみます。
\[x\frac{dy}{dx}+y=0\]
これは変数分離によって簡単に解くことができますが、ここでは少し違ったやり方で解いてみます。両辺に $dx$ をかけると
\[xdy+ydx=0\]
となります。左辺をじっと見つめると、これは $xy$ の全微分になっていることに気づきます。念のために確認しておくと、
\[d(xy)=\frac{\partial (xy)}{\partial x}dx+\frac{\partial (xy)}{\partial y}dy=xdy+ydx\]
確かに $xdy+ydx$ は $xy$ の全微分ですね。すると微分方程式は
\[d(xy)=0\]
と書き直せるので、積分すると
\[xy=c\]
という解が得られます。$xy$ という関数を目視で見つけることができるなら、変数分離よりも早く、しかも暗算で解いてしまうことができます。
一般に次のような形の方程式
\[d\varPhi=P(x,y)dx+Q(x,y)dy=0\tag{A}\]
において、関数 $P(x,y)$ と $Q(x,y)$ が
\[\frac{\partial \varPhi}{\partial x},\quad\frac{\partial \varPhi}{\partial y}\tag{A1}\]
のように、ある関数 $\varPhi$ の偏微分の形で与えられているとき、(A) を完全微分型方程式とよび、その解は
\[\varPhi (x,y)=c\tag{A2}\]
で与えられます ($c$ は任意定数)。もちろんこのような $\varPhi$ がいつでも存在するとは限らないし、あったとしても見つけることが難しい場合もあります。とはいえ目視で $\varPhi$ を見つける以外にもある程度の手掛かりはあります。その1つは (A) が完全微分型であるための必要十分条件が
\[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\tag{A3}\]
であるという定理です。これを満たさなければ $\varPhi$ は存在しません。まずは必要条件、すなわち
\[\frac{\partial\varPhi}{\partial x},\quad\frac{\partial\varPhi}{\partial y}\tag{A1}\]
を満たす $\varPhi$ が存在するならば、
\[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\tag{A3}\]
となることを証明してみます。これは簡単です。
\[\frac{\partial P}{\partial y}=\frac{\partial^2\varPhi}{\partial y\partial x},\quad\frac{\partial Q}{\partial x}=\frac{\partial^2\varPhi}{\partial x\partial y}\]
となるので、微分の順序を入れ替えれば (A3) が成立します。今度は十分条件、すなわち
\[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\tag{A3}\]
が成立するならば、
\[\frac{\partial\varPhi}{\partial x},\quad\frac{\partial\varPhi}{\partial y}\tag{A1}\]
を満たす $\varPhi$ が存在することを証明します。
\[\varPhi (x,y)=\int_{a}^{x}P(s,y)ds+R(y)\tag{A4}\]
とおくと、
\[\begin{align*}\frac{\partial\varPhi}{\partial y}&=\int_{a}^{x}\frac{\partial P(s,y)}{\partial y}ds+\frac{dR}{dy}\\[6pt]&=Q(x,y)-Q(a,y)+\frac{dR}{dy}\end{align*}\]
となります。$\partial\varPhi/\partial y=Q(x,y)$ となるには
\[\frac{dR}{dy}=Q(x,y)\]
が満たされている必要があります。積分して
\[R=\int_{b}^{y}Q(a,t)dt+c\]
これを (A4) に代入して
\[\varPhi (x,y)=\int_{a}^{x}P(s,y)ds+\int_{b}^{y}Q(a,t)dt+c\]
ここで $x=a,\:y=b$ とおくと積分定数が $c=\varPhi (a,b)$ と定まり
\[\varPhi (x,y)=\int_{a}^{x}P(s,y)ds+\int_{b}^{y}Q(a,t)dt+\varPhi (a,b)\tag{A5}\]
という表式を得ます。この積分は下の図の A → S → B という経路に沿っています。
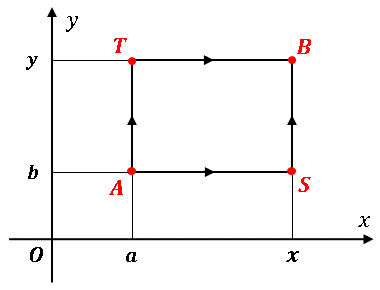
これを A → T → B という経路に変えても積分結果は変わらないので、(A5) は
\[\varPhi (x,y)=\int_{a}^{x}P(s,b)ds+\int_{b}^{y}Q(x,t)dt+\varPhi (a,b)\tag{A6}\]
としてもかまいません。
積分因子
与えられた方程式が完全微分型でなくても、ある関数 $\mu (x,y)$ をかけて
\[\mu (x,y)P(x,y)dx+\mu (x,y)Q(x,y)dy=0\tag{B}\]
としたものが完全微分型方程式になるとき、$\mu (x,y)$ を 積分因子 とよびます。もちろんその必要十分条件は
\[\frac{\partial\mu P}{\partial y}=\frac{\partial\mu Q}{\partial x}\tag{B}\]
となります。しかし一般にこの方程式から具体的な $\mu (x,y)$ を発見するのは難しく、試行錯誤しなければならない場合がほとんどです。比較的簡単なケース、すなわち $\mu$ が $x$ または $y$ だけに依存する場合、あるいは $\mu (x,y)=x^my^m$ という形になっている場合には、解法が定型化されていますので、以下の演習問題で順次取り上げることにします。
【DE08】完全微分型方程式①
$(Ax+By+C)dx+(Bx+Cy+D)dy=0$ の一般解を求めてください。
【ヒント】この問題については $\varPhi$ の形をある程度予測できれば簡単に解けてしまいます。
【解答】与えられた微分方程式
\[(Ax+By+C)dx+(Bx+Cy+D)dy=0\tag{A}\]
が完全微分型であるためには、
\[P(x,y)=Ax+By+C,\quad Q(x,y)=Bx+Cy+D\]
について
\[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\]
という条件式を満たしている必要があります。実際に計算してみると
\[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}=B\]
となるので、(A) は完全微分型方程式であり、
\[\frac{\partial \varPhi}{\partial x},\quad\frac{\partial \varPhi}{\partial y}\]
を満たすような $\varPhi$ が存在することになります。そして、そのような $\varPhi$ は
\[\varPhi=\int_{a}^{x}P(s,y)ds+\int_{b}^{y}Q(a,t)dt+\Phi (a,b)+E\]
によって与えられます ($E$ は定数)。実際に計算してみると
\[\begin{align*}\varPhi&=\int_{a}^{x}(As+By+C)ds+\int_{b}^{y}(Ba+Ct+D)dt\\[6pt]&=\frac{A}{2}x^2+Bxy+Cx+\frac{C}{2}y^2+Dy+F\end{align*}\]
となります。ただし定数項は $F$ にまとめておきました。一般解は $\varPhi=c$ で与えられるので、あらためて $G$ を定数として
\[\frac{A}{2}x^2+Bxy+Cx+\frac{C}{2}y^2+Dy+G=0\tag{A1}\]
が求める解となります。
【別解】ところが、この問題では与えられた方程式
\[(Ax+By+C)dx+(Bx+Cy+D)dy=0\tag{A}\]
をよくみると、$x$ で微分して $Ax$ という項になるし、$y$ で微分して $Cy$ という項が現れるのだから、$k,\:l,\:m$ を定数として
\[\varPhi=\frac{A}{2}x^2+\frac{C}{2}y^2+kxy+lx+my=0\]
という形になるだろうと予測できます。試しに偏微分してみると
\[\begin{align*}\frac{\partial \varPhi}{\partial x}&=Ax+ky+l\\[6pt]\frac{\partial \varPhi}{\partial y}&=Cy+kx+m\end{align*}\]
となるので、(A) と係数を比較して
\[k=B,\quad l=C,\quad m=D\]
がわかります。したがって
\[\frac{A}{2}x^2+Bxy+Cx+\frac{C}{2}y^2+Dy+G=0\]
という一般解を得られます。
【DE09】完全微分型方程式②
(1) 次のような形の微分方程式
\[\mu (x,y)P(x,y)dx+\mu (x,y)Q(x,y)dy=0\]
が与えられたとき、方程式が $d\varPhi=0$ すなわち完全微分型になるための必要十分条件は
\[\frac{\partial (\mu P)}{\partial y}=\frac{\partial (\mu Q)}{\partial x}\]
であることが知られています。積分因子 $\mu$ が $x$ のみに依存する関数であるとき、
\[\mu (x)=\exp\left[\int\frac{1}{Q}\left(\frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}\right)dx\right]\]
で与えられることを示してください。
(2) 微分方程式 $(x+ky)dx+xdy=0$ を解いてください ($k$ は定数)。
【解答】(1) 積分因子 $\mu$ が $x$ の関数 $\mu (x)$ であるとき、完全微分型になるための必要十分条件
\[\frac{\partial (\mu P)}{\partial y}=\frac{\partial (\mu Q)}{\partial x}\]
を書きなおすと
\[\mu\frac{\partial P}{\partial y}=Q\frac{d\mu}{dx}+\mu\frac{\partial Q}{\partial x}\]
となります。これを整理すると
\[\frac{1}{Q}\left(\frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}\right)=\frac{1}{\mu}\frac{d\mu}{dx}\]
となります。右辺が $x$ だけの関数ですから、もちろん左辺も $x$ の関数です。よって、この式を積分して
\[\mu (x)=\exp\left[\int\frac{1}{Q}\left(\frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}\right)dx\right]\]
となります。
(2) 与えられた微分方程式
\[(x+ky)dx+xdy=0\]
において
\[\frac{1}{Q}\left(\frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}\right)\]
を計算すると
\[\frac{1}{Q}\left(\frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}\right)=\frac{k-1}{x}\]
となります。右辺は $x$ だけの関数なので、
\[\mu(x)=\exp\int\left(\frac{k-1}{x}\right)dx=|x|^{k-1}\]
となります($k=1$ のとき、すなわち $\mu$ が定数のときもこの形で表せます)。したがって $\mu (x)=x^{k-1}$ を
\[(x+ky)dx+xdy=0\]
の両辺にかけると
\[x^kdx+kx^{k-1}ydx+x^kdy=0\]
この式の左辺は微分型になっているはずです。変形していくと
\[\begin{align*}&d\left(\frac{x^{k+11}}{k+1}\right)+kyd\left(\frac{x^k}{k}\right)+k^kdy=0\\[6pt]&d\left(\frac{x^{k+1}}{k+1}\right)+d(x^ky)=0\end{align*}\]
これを積分して整理すると
\[x^{k+1}+(k+1)x^ky=A\]
という解を得ます。
【DE10】完全微分型方程式③
微分方程式 $(y^3+x^2y)dx+(x^3-y^2)dy=0$ を解いてください。
【ヒント】まずは左辺が完全微分型になっているかどうかを確認します。なっていなければ積分因子 $\mu$ を見つけます。
【解答】微分方程式
\[(y^3+x^2y)dx+(x^3-y^2)dy=0\tag{A}\]
が完全微分型であるためには、
\[P(x,y)=y^3+x^2y,\quad Q(x,y)=x^3-y^2\]
について
\[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\]
という条件式を満たしていなければなりませんが、計算してみると
\[\begin{align*}\frac{\partial P}{\partial y}=3y^2+x^2\\[6pt]\frac{\partial Q}{\partial x}=3x^2-y^2\end{align*}\]
となるので、与えられた微分方程式は完全微分型ではありません。そこで
\[\frac{\partial (\mu P)}{\partial y}=\frac{\partial (\mu Q)}{\partial x}\]
となるような積分因子 $\mu$ を見つける必要があります。$\mu=x^my^n$ とおくと
\[\begin{align*}\mu P=x^my^{n+3}+x^{m+2}y^{n+1}\\[6pt]\mu Q=x^{m+3}y^n-x^{m+1}y^{n+2}\end{align*}\]
それぞれ $x$ , $y$ で微分すると
\[\begin{align*}\frac{\partial (\mu P)}{\partial y}&=(n+3)x^my^{n+2}+(n+1)x^{m+2}y^n\\[6pt]\frac{\partial (\mu Q)}{\partial x}&=(m+3)x^{m+2}y^n-(m+1)x^my^{n+2}\end{align*}\]
両辺の係数を比較すると
\[\begin{align*}n+3=-m-1\\[6pt]n+1=m+3\end{align*}\]
これを解いて
\[m=-3,\quad n=-1\]
が得られます。すなわち
\[\mu=\frac{1}{x^3y}\]
となります。これを微分方程式
\[(y^3+x^2y)dx+(x^3-y^2)dy=0\]
にかけて
\[\left(\frac{y^2}{x^3}+\frac{1}{x}\right)dx+\left(\frac{1}{y}-\frac{y}{x^2}\right)dy\]
これを変形していくと
\[\begin{align*}-\frac{1}{2}y^2d\left(\frac{1}{x^2}\right)+d(\log x)+d(\log y)-\frac{1}{2}\frac{1}{x^2}d(y^2)=0\\[6pt]d(\log xy)-\frac{1}{2}\left\{y^2d\left(\frac{1}{x^2}\right)-\frac{1}{x^2}d(y^2)\right\}=0\\[6pt]d(\log xy)-\frac{1}{2}d\left(\frac{y^2}{x^2}\right)=0\end{align*}\]
これを積分して一般解
\[\log xy=\frac{y^2}{2x^2}+C\]
が得られます。
【DE11】変数分離型微分方程式の積分因子
変数分離型の微分方程式
\[\frac{dy}{dx}=F(x)G(y)\quad (Y\neq 0)\]
を完全微分型方程式
\[\mu P(x,y)dx+\mu Q(x,y)dy=0\]
の形にするための積分因子 $\mu$ を求めてください。ただし $\mu$ は
\[\frac{\partial (\mu P)}{\partial y}=\frac{\partial (\mu Q)}{\partial x}\]
をみたす関数です。
【ヒント】まずは与えられた方程式を変形します。
【解答】微分方程式
\[\frac{dy}{dx}=F(x)G(y)\quad (Y\neq 0)\]
を変形すると
\[F(x)G(y)dx-dy=0\tag{A}\]
となります。すなわち
\[P=FG,\quad Q=-1\]
とみると、(A) が完全微分型であるためには
\[\frac{\partial (\mu FG)}{\partial y}=\frac{\partial (-\mu)}{\partial x}\]
とみたす必要があります。ここで仮に $\mu$ が $y$ だけの関数であると仮定すると、右辺は 0 ですから
\[F\left(\frac{d\mu}{dy}G+\mu\frac{dG}{dy}\right)=0\]
となります。すなわち
\[\frac{d\mu}{dy}G+\mu\frac{dG}{dy}=0\]
となるような $\mu$ を見つければよいことになります。変数分離すると
\[\frac{d\mu}{d\mu}=-\frac{dG}{dG}\]
これを積分して、任意定数を $A$ とすると
\[\log\mu=\log\frac{A}{G}\]
となります。すなわち積分因子のひとつとして
\[\mu=\frac{1}{G}\]
が得られます。

エクセルや数学に関するコメントをお寄せください