度数分布表
母集団から抽出した標本から有用な情報を得るためには、標本を整理する必要があります。たとえば数値を大きさの順に並べて、全体を適当な幅の区間に切り分けて、それぞれの区間に入る標本の個数を数えます。この区間のことを階級、階級の中から選んだ代表的な値を標識(階級値)とよびます。多くの場合に標識には区間の中間値が選ばれます。また区間ごとの標本の個数を 度数(frequency) とよびます。階級、標識、度数を整理して表にしたものを 度数分布表(frequency table)といいます。
ある学校の1学年の数学テストの得点分布表の度数分布表が以下のように用意されているとします。
| データ区間 | 標識 | 度数 | 累積度数 |
|---|---|---|---|
| 0 – 10 | 5 | 0 | 0 |
| 10 – 20 | 15 | 0 | 0 |
| 20 – 30 | 25 | 1 | 1 |
| 30 – 40 | 35 | 4 | 5 |
| 40 – 50 | 45 | 11 | 16 |
| 50 – 60 | 55 | 26 | 42 |
| 60 – 70 | 65 | 25 | 67 |
| 70 – 80 | 75 | 20 | 87 |
| 80 – 90 | 85 | 11 | 98 |
| 90 – 100 | 95 | 2 | 100 |
たとえば “20 – 30” は 20 点以上 30 点未満を表し、上限 30 を含んでいません。また標識はその中間値 25 としています。右端のデータ(累積度数)は各階級までの累積人数です。つまり「その点数以下の生徒は何人いるか」を示しています。
標本平均と標本分散
標本の大きさが $N$ で、標本の値が $x_1,\:x_2,\:\cdots,\:x_n$ であるとき、
\[\bar{x}=\frac{1}{N}\sum_{i=1}^{N}x_i=\frac{1}{N}(x_1+x_2+\cdots+x_N)\]
を 標本平均 といいます。期待値 $\mu$ が全体の情報(確率分布)を得た上での「真の平均値」であるのに対して、標本平均 $\bar{x}$ は母集団から取り出した標本の中における「部分的な平均値」です。標本のばらつき具合を示す量として 標本分散 を次のように定義します。
\[s^2=\frac{1}{N}\sum_{i=1}^{N}(x_i-\bar{x})=\frac{1}{N}[(x_1-\bar{x})^2+(x_2-\bar{x})^2+\cdots+(x_N-\bar{x})^2]\]
標本分散の平方根 $s$ を標本標準偏差とよびます。記事冒頭で使用したサンプル「数学テストの得点分布表」において、標本平均と標本分散、標本分散を計算すると
\[\bar{x}=63.32,\quad s^2=201.80,\quad s=14.21\]
となります。
中央値と最頻値
標本のちょうど中央の値を中央値(メジアン)と定義します。標本の大きさが奇数のときはちょうど中央にある値を、偶数のときは中央にある2つの値の平均値をとります。「数学テストの得点分布表」で数値を小さい順に並べると、中央に 62 という値が2つ並ぶので、中央値は $(62+62)/2=62$ となります。
度数のもっとも大きい階級の標識を最頻値(モード)と定義します。「数学テストの得点分布度数表」を見ると、標識 55 の度数が 26 で最大となっているので最頻値は 55 です。
度数分布表をグラフにします
度数分布を柱状のグラフで表したものをヒストグラムといいます。また、ヒストグラムの長方形の上辺の中点を結んだ折れ線グラフを度数折れ線とよびます。「数学テストの得点分布度数表」をヒストグラム、および度数折れ線にすると次のようになります。
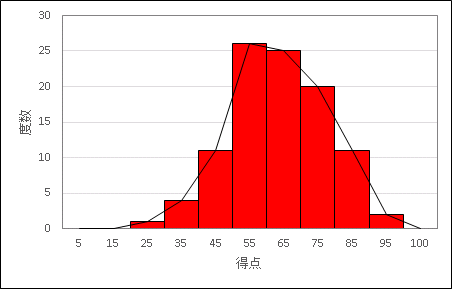
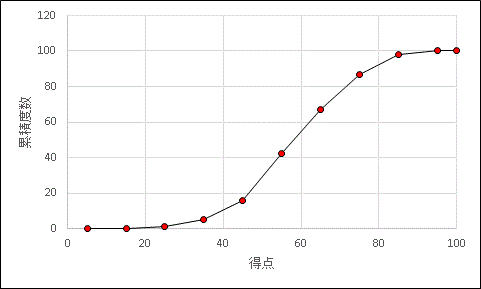
累積度数をグラフに表したものを累積度数折れ線とよびます。「数学テストの得点分布度数表」を累積度数折れ線にすると下の図のようになります。

エクセルや数学に関するコメントをお寄せください