フーリエ変換（非周期関数の展開式）

フーリエ変換

フーリエ変換

周期 $2L$ をもつ関数 $f(x)$ は離散係数 $c_n$ を用いて
\[\begin{align*}f(x)&=\sum_{n=-\infty}^{\infty}c_n\exp\left(\frac{in\pi x}{L}\right)\\[6pt]c_n&=\frac{1}{2L}\int_{-L}^{L}f(t)\exp\left(\frac{-in\pi t}{L}\right)\end{align*}\]
とフーリエ級数展開できます。ここで $L\rightarrow \infty$ の極限をとれば、非周期関数の展開式も得られるはずです。そこで係数 $c_n$ を $f(x)$ の展開式に代入し、
\[\omega_n=\frac{n\pi}{L},\quad \Delta\omega=\omega_n-\omega_{n-1}=\frac{\pi}{L}\]
とおくと、
\[f(x)=\frac{1}{2\pi}\sum_{n=-\infty}^{\infty}\left[ \int_{-L}^{L}f(t)e^{-i\omega_nt}dt\right]e^{i\omega_nx}\Delta\omega\]
という表式が得られます。$L\rightarrow \infty$ とすれば総和の記号が積分に変わって
\[f(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega\int_{-\infty}^{\infty}f(t)e^{-i\omega (t-x)}dt\]
となります。これをフーリエ積分公式とよびます。そして
\[F(\omega)=\int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt\]
とおけば、
\[f(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{i\omega x}d\omega\]
と表すことができます。変数 $t$ をあらためて $x$ に置き直すと、

\[F(\omega)=\int_{-\infty}^{\infty}f(x)e^{-i\omega x}dx\tag{A}\]\[f(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{i\omega x}d\omega\tag{B}\]

となります。つまり $f(x)$ から $F(\omega)$ を求めることができて、またその逆に $F(\omega)$ から $f(x)$ を求めることができます。そこで $F(\omega)$ を $f(x)$ のフーリエ変換、$f(x)$ を $F(\omega)$ のフーリエ逆変換とよびます。変換の対称性を考慮して係数を $1/\sqrt{2\pi}$ とした

\[F(\omega)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(x)e^{-i\omega x}dx\tag{C}\]\[f(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}F(\omega)e^{i\omega x}d\omega\tag{D}\]

という表式もよく用いられます。より簡略的に
\[\begin{align*}F(\omega)=\mathcal{F}[f(x)]\\[6pt]f(x)=\mathcal{F}^{-1}[F(\omega)]\end{align*}\]
と表すこともあります。

単一矩形波のフーリエ変換

例として $\mid x\mid\leq d$ の範囲にだけ存在する波（単一矩形波）
\[f(x)=\begin{cases}\displaystyle\frac{1}{2d} & (\mid x\mid\leq d)\\[6pt]0 & (\mid x\mid\gt d)\end{cases}\]
をフーリエ変換してみます。

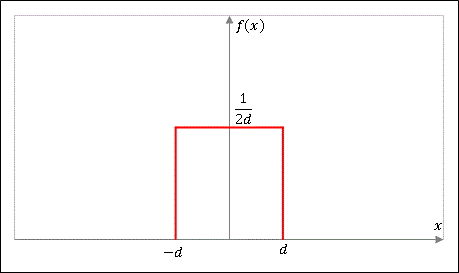
Excel単一矩形波のフーリエ変換

定義にしたがって $F(\omega)$ を計算してみると
\[F(\omega)=\int_{-\infty}^{\infty}f(x)e^{-i\omega x}dx=\frac{\sin\omega d}{\omega d}\]
となります。$\omega$ の変化に対する $F(\omega)$ を図示すると次のようになります。

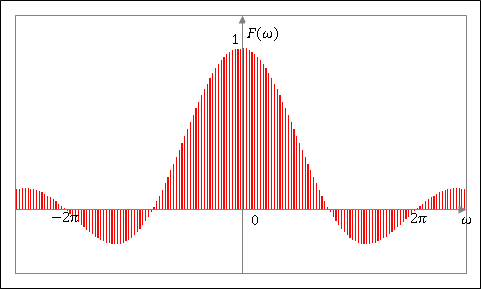
Excel連続スペクトル

原点でピーク 1 をとり左右に減衰しています。これは $f(x)$ が $\omega=0$ , すなわち $y=1$ という波（というより直線）を成分として最も多く含んでおり、$\omega$ の絶対値が大きくなるほど $e^{i\omega x}$ の寄与が小さくなっていくことを示しています。このように、$F(\omega)$ はフーリエ級数の係数 $c_n$ と本質的に全く同じものであり、関数 $f(x)$ の中に、ある角振動数 $\omega$ の波 $e^{i\omega x}$ をどれだけ含んでいるかを示すものです。そうした意味で $F(\omega)$ のことを連続スペクトルとよぶことがあります。　

フーリエ変換の基本性質

以下にフーリエ変換の基本的性質を載せておきます。いずれも定義にしたがって簡単に導けるので証明は省略します。

$f(x)$ と $g(x)$ のフーリエ変換をそれぞれ
\[\mathcal{F}[f(x)]=F(\omega),\quad \mathcal{F}[g(x)]=G(\omega)\]とするとき、以下の式が成り立つ。

① 共役関数の変換
\[\mathcal{F}[f^*(x)]=F^*(-\omega)\tag{E}\]

② 重ね合わせの原理
\[\mathcal{F}[af(x)+bg(x)]=aF(\omega)+bF(\omega)\tag{F}\]

③ 尺度変換
\[\mathcal{F}[f(ax)]=\frac{1}{\mid a\mid}F\left( \frac{\omega}{a}\right)\quad (a\neq 0)\tag{G}\]

④ 対称性
\[\mathcal{F}[F(\omega)]=2\pi f(-x)\tag{H}\]

⑤ 周波数シフト
\[\mathcal{F}[f(t)e^{i\omega t}]=F(\omega-\omega_0)\tag{I}\]

⑥ 時間軸移動
\[\mathcal{F}[f(t-t_0)]=F(\omega)e^{-i\omega t_0}\tag{J}\]

工学・物理学等への応用で分かりやすいように、⑤ と ⑥ では変数 $x$ を時間を表す変数 $t$ に書き換えてあります。

フーリエ変換の微分

$f(x)$ のフーリエ変換
\[f(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{i\omega x}d\omega\]
を $x$ について微分すると
\[f'(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)(i\omega)e^{i\omega x}d\omega\]
となります。これは $f'(x)$ のフーリエ変換が
\[\mathcal{F}[f'(x)]=i\omega F(\omega)\]
となることを表しています。$n$ 回微分すると
\[\mathcal{F}[f^{(n)}(x)]=(i\omega)^n F(\omega)\tag{K}\]
となります。