直線と線分・平角・補角・対頂角

直線と線分、半直線

直線（Line）

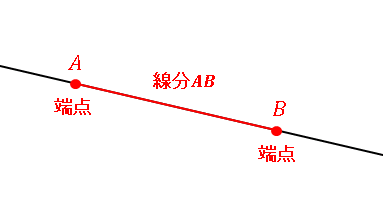
平面において、$2$ 点 $A,\:B$ を通り、端のない線のことを 直線 (line) $AB$ とよびます。「端がない」とは「無限にどこまでも続いている」ということです。

線分（Segment）

$A$ と $B$ に挟まれた部分は線分または 有限直線とよび、$AB$ で表します。このとき、点 $A$ と $B$ のことを線分の端といい、線分 $AB$ の長さは $AB$ によって表されます。

半直線（Half-line）

　
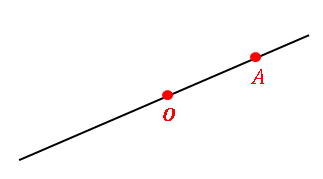
　直線上の任意の場所に $1$ 点 $O$ をとると、直線は $2$ つの部分に分けられます。分割されたそれぞれの部分を 半直線 とよび、点 $O$ を半直線の端点といいます。半直線が点 $A$ を通るとき、この半直線を半直線 $OA$ のように表します。

平角・補角・対頂角

平角（Straight angle）

　
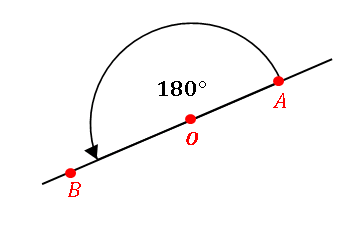
　$3$ 点 $A,\:O,\:B$ が一直線上にあるとき、半直線 $OA$ と $OB$ は角をなすと考えて、$\angle AOB$ を 平角 とよびます。直線は平面を二等分するので、平角は $180^\circ$ です。

補角（Supplement）

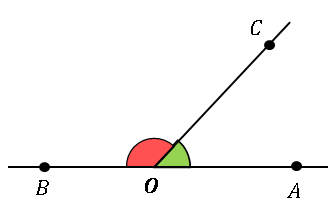
図のように、点 $C$ から直線 $AB$ の上まで線分を引いたとき、$\angle AOC$ と $\angle COB$ を加えると平角に等しくなります。すなわち
 \[\angle AOC+\angle COB=2\angle R\]
です。このとき、$\angle AOC$ は $\angle COB$ の補角である、$\angle COB$ は $\angle AOC$ の補角 であるといいます。

対頂角（Vertical Angle）

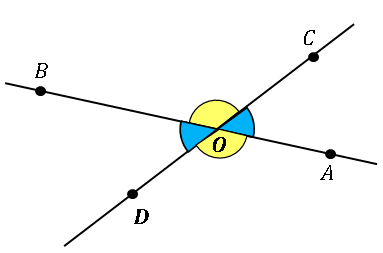
図のように、直線 $AB$ と $CD$ が点 $O$ で交わるとき、$\angle AOC$ と $\angle BOD$ は 対頂角である、$\angle AOD$ と $\angle BOC$ の対頂角 であるといいます。このとき
 \[\begin{align*}&\angle AOC+\angle AOD=2\angle R\\[6pt]&\angle AOD+\angle BOD=2\angle R\end{align*}\]
が成り立つので、
 \[\angle AOC=\angle BOD\]
となります。すなわち「対頂角は等しい」という定理が成り立ちます。

平行と垂直

平行（parallel）

$2$ 本の直線が互いに交わらないとき、この二直線は互いに平行であるといいます。

垂直（Perpendicular）

図のように二直線が交わって、
 \[\angle AOB=\angle COB=90^\circ\]
であるとき、$\angle AOB$ は直角であるといいます（もちろん $COB$ も直角です）。このとき直線 $OA$ は直線 $OB$ に対して垂直であるといいます。同様に線分 $OA$ は線分 $OB$ に対して垂直であるといいます。